Карл Левитин - Геометрическая рапсодия

16

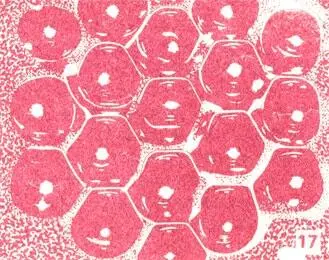
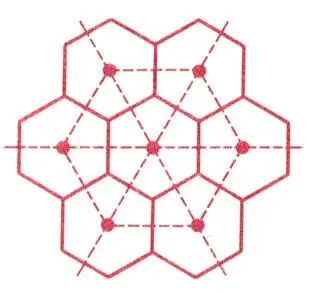
Первое разумное суждение о том, в чем загадка правильной формы кристаллов, было высказано, видимо, Иоганном Кеплером в трактате "О шестиугольном снеге". Оно относится к снежинкам. Почему они всегда шести-лучевые или шестиугольные? — спрашивал он себя. И пришел к гениальному для тех времен выводу: потому, что невидимые капельки водяного пара шарообразны и на холоде приклеиваются друг к другу таким образом, что каждая сцепляется с двенадцатью другими, "подобно зернам граната". Это было в начале XVII века и никто еще не сумел заглянуть внутрь вещества, и даже Ньютон еще не затеял своего спора с Грегори о целующихся сферах.

"Чтобы познать невидимое, смотри внимательно на видимое" — сказано в одной древней книге. сознательно или подсознательно этому принципу следовали все ученые, которым предстояло заложить фундамент новой науки — кристаллографии. Французский минералог Рене Жюст Гаюи однажды случайно уронил кристалл известкового шпата. Подобрав кусочки, он увидел, что они в точности повторяют форму разбившегося кристалла. Заинтригованный, он стал один за другим разбивать кристаллы из своей огромной коллекции и, как писал впоследствии его биограф, "продолжая трудиться на этом поприще, сделался основателем кристаллографии".

Вместе с тем, правда, Гаюи получил и насмешливое прозвище "кристаллокласт" — "разрушитель кристаллов", которое присвоили ему коллеги, предпочитавшие умозрительный подход к проблеме кристаллов слишком уж, на их взгляд, грубому натурному эксперименту. Но прошли долгие десятилетия, прежде чем почти одновременно Е. С. Федоров в России и А. Шенфлис в Германии, независимо друг от друга — один шел геометрическим путем, а другой воспользовался алгебраическим аппаратом теории групп — вывели все возможные в пространстве группы симметрии, которые определяют собой и все разнообразие кристаллических форм в природе. Любопытно, что когда они сверили результаты своих работ, то оказалось, что Федоров насчитал 229 возможных способов сочетания частиц в кристалл, а Шенфлис — 227. Федоров пропустил один способ, замеченный Шенфлисом, но тот зато проглядел целых три, указанных Федоровым. Немедленный обмен письмами позволил исправить недосмотры, и с тех пор в кристаллографии твердо установлено, что федоровских групп ровно 230.

17

"Все мои работы — это игры, серьезные игры", — говорил о себе голландский художник Мауриц Корнелис Эсхер, гравюрами которого иллюстрирована не только эта, но и множество других книг, вышедших в разных странах и так или иначе связанных с наукой. Исследования Федорова и Шенфлиса тоже довольно долго рассматривались как некие математические забавы и развлечения, не имеющие отношения к правде жизни. Еще Рентген не открыл своих знаменитых лучей, Беккерель — радиоактивности, Томсон — электрона и, наконец, Лауэ не обнаружил рассеяния рентгеновских лучей кристаллами. Все эти события должны были произойти для того, чтобы федоровские группы легли в основу точного и математически строгого расчета архитектуры кристаллов.

"Федоровская группа — это лишь канва, по которой природа может вышивать бесконечно разнообразные узоры атомных расположений. Но типов канвы всего 230, и великая заслуга Федорова и Шенфлиса заключается в том, что они установили этот факт и перечислили все возможные случаи. Чтобы в полной мере оценить удивительную проницательность, которую проявили эти ученые при выводе пространственных групп, нужно иметь в виду, что в те времена действительное расположение атомов в кристаллах совершенно не было известно". Цитата взята из книги П. М. Зоркого "Архитектура кристаллов". В ней автор позволил себе любопытное признание: "По-видимому, в последнее время несколько изменились функции научно-популярной литературы. Стремительное увеличение объема научных знаний часто не позволяет ученым и инженерам следить за развитием смежных областей науки, пользуясь специальными статьями и монографиями. Слишком много времени и сил требует основная работа. На помощь приходит научно-популярная литература. Она дает возможность сохранять широту кругозора, а иногда (автор знает об этом по собственному опыту) может пригодиться в основной работе".

Слова эти, написанные в наше время, в конце шестидесятых годов, едва ли вызвали бы возражение и в прежние времена. Евграф Степанович Федоров начал работать над своей первой монографией "Начала учения о фигурах" шестнадцатилетним гимназистом. И еще шестнадцать лет прошло, прежде чем он ее кончил. Причиной тому, видимо, не одна лишь необычная фундаментальность мышления, которая замечалась у будущего академика Петербургской академии наук. Виной тому и популярная литература, которая сбила его с прямого математического пути, заставила заинтересоваться кристаллографией, поступить в Горный институт, закончить его и потерять возможность разграничивать математику и кристаллографию на "основную" и "смежную" науки.

Нечто похожее случилось и с Маурицем Корнелисом Эсхером.

"В наше время, когда искусство и наука живут в различных областях духовной жизни и при этом стремятся разойтись все дальше и дальше друг от друга, столь удивительно вдруг встретить художника, который в своей творческой деятельности занят проблемами, лежащими в основании целых наук и нескольких математических дисциплин. подобное не случалось с тех времен, когда художники открывали законы перспективы и были пионерами в анатомических исследованиях", — пишет во введении к своей книге "Проблемы симметрии в периодических рисунках М. К. Эсхера" профессор Амстердамского университета Каролина Генриетта Мак-Гиллаври. Книга эта, состоящая из более чем сорока работ художника и соответствующего кристаллографического толкования их, служит учебным пособием для студентов.

"Я часто удивлялся своей мании создавать периодические рисунки, — писал сам художник. — Однажды я спросил своего друга, психолога, в чем причина моей увлеченности ими, но его ответ, что меня ведет здесь примитивный инстинкт повторения сделанного, ничего не объяснил".

18

И в самом деле, каким инстинктом объяснить поразительную по плавности перехода от рыбы, плывущей в темных глубинах моря, к птице, летящей в прозрачной высоте, гравюру "Небо и вода. I" или четкую в своем стремлении связать живое с неживым гравюру "Рептилии"? А ведь обе они построены на "повторении сделанного".