Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

В одной из старейших телевизионных игр под названием Let's Make a Deal участникам предлагают сделать слепой выбор. Случайно выбранный зритель выходит на сцену и видит перед собой три двери, за одной из которых находится автомобиль, а за двумя другими — ослы. Участник надеется выбрать ту дверь, за которой спрятан автомобиль, а не ту, где стоит осел. Если он угадывает, то получает автомобиль в качестве приза. Однако не все так просто. После того, как участник сделает выбор, ведущий, Монти Холл, который знает, за какой дверью находится автомобиль, показывает одного из ослов (не открывая две оставшиеся двери) и спрашивает участника, хочет ли он оставить первоначальный выбор (что кроется за ним пока неизвестно) или, может быть, передумает и выберет другую неоткрытую дверь. В этот момент, чтобы повысить напряжение, публика начинает скандировать «оставить» или «передумать». Вопрос в том, что делать? Есть ли разница? Если так, то какую стратегию лучше использовать (т. е. что может повысить вероятность выигрыша)?

Кто-то скажет, что лучше всего принимать решение интуитивно. Большинство, однако, придерживаются мнения, что в любом случае разницы никакой нет, поскольку у вас один шанс из двух получить автомобиль. И те и другие неправы, а раз так, то есть серьезный мотив, разобраться что к чему.

Лучше всего рассмотреть эту задачу шаг за шагом, а потом, для уверенности, рассмотреть экстремальную ситуацию и принять решение.

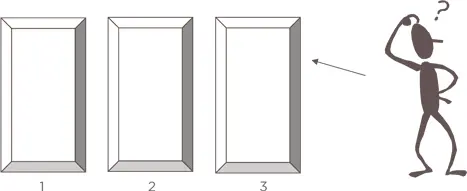
Разберем задачу шаг за шагом. Результат постепенно станет ясным. За дверями находятся два осла и один автомобиль . Вы должны попытаться получить автомобиль. Вы выбираете дверь 3. Монти Холл открывает одну из дверей, которую вы не выбрали , и показывает осла.

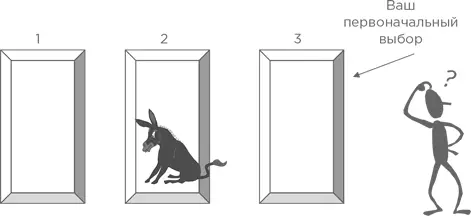
Он спрашивает: «Вы все еще хотите оставить свой первоначальный выбор или передумаете и выберете другую закрытую дверь?» Чтобы помочь принять решение, воспользуемся стратегией анализа экстремальных ситуаций. Допустим, у нас 1000 дверей, а не три.

Вы выбираете дверь 1000. Какова вероятность того, что это правильная дверь?

« Очень маловероятно», поскольку вероятность выбора правильной двери равна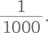

Насколько вероятно, что автомобиль находится за одной из других дверей (1–999)?

« Очень вероятно»: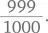

Это все « очень вероятные» двери!

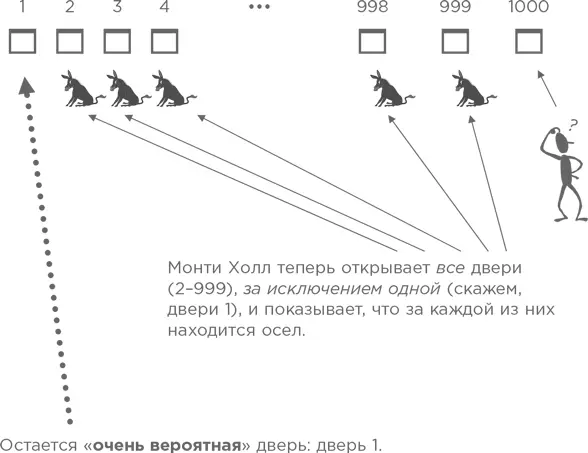
Теперь мы готовы ответить на вопрос. Какой выбор будет наилучшим?

• Дверь 1000 (« очень маловероятная » дверь) или

• Дверь 1 (« очень вероятная » дверь)?

Ответ теперь очевиден. Мы должны выбрать «очень вероятную» дверь, т. е. «передумать» — это лучшая стратегия для участника шоу. В экстремальной ситуации намного легче увидеть лучшую стратегию, чем при анализе ситуации с тремя дверями, как в исходных условиях задачи. Принцип одинаков в любой ситуации.

Эта задача вызвала немало споров в научных кругах и даже попала на страницы газеты The New York Times и других популярных изданий. Джон Тирни написал в The New York Times (Sunday, July 21, 1991), что «возможно это только иллюзия, однако похоже спору, в котором участвовали все от математиков до читателей журнала Parade и любителей телеигры Let's Make a Deal, положен конец. Спор начался, когда Мэрилин вос Савант опубликовала головоломку в журнале Parade . Как известно читателям ее колонки „Спросите Мэрилин“, имя г-жи вос Савант включено в списки Галереи славы Книги рекордов Гиннесса за обладание „наивысшего IQ“. Но этот факт производит на публику не такое впечатление, как то, что она сумела ответить на вопрос читателя». Мэрилин дала правильный ответ, и, хотя многие математики продолжают спорить, мы решили эту задачу!

Некоторые задачи на первый взгляд кажутся чрезвычайно сложными. Смутить могут, например, очень большие числа. А иногда в замешательство приводит излишнее количество данных, некоторые из которых совершенно не нужны для решения. Даже формулировка задачи способна поставить в тупик. Что бы там ни было, отличный подход — упростить задачу, однако так, чтобы она осталась эквивалентной исходному варианту. Попробуйте уменьшить числа, изменить рисунок или как-то иначе упростить задачу. Решая упрощенную версию, вы получаете представление о том, как справиться с исходной задачей.

Купив первый раз новый компьютер, вы ведь не брались за освоение сразу всех функций и возможностей, а, скорее всего, начинали с чего-то более знакомого и постепенно добавляли новое, пока не выясняли, на что способно приобретение. Наверняка вы брались сначала за более простые функции.

Допустим, вам нужно решить следующую задачу:

Дано 19 последовательных целых чисел, сумма которых равна 95. Какое число стоит на десятом месте в этом ряду?

Одни, скорее всего, попробуют применить алгебраический подход и представят 19 целых чисел, как x , ( x + 1), ( x + 2), ( x + 3), …, ( x + 17), ( x + 18) и так далее. Так они дойдут до 95, а потом найдут решение для x . Другие заметят, что число в десятой позиции является средним, обозначат его как x и представят остальные числа следующим образом: ( x + 9), ( x + 8), ( x + 7), …, ( x − 7), ( x − 8), ( x − 9). Теперь можно объединять парные члены по мере их добавления, т. е. преобразовывать ( x − 9) и ( x + 9) в 2 x , ( x − 8) и ( x + 8) тоже в 2 x и т. д., получая каждый раз 2 x . Такая версия намного проще для решения, поскольку мы получаем уравнение вида 9(2 x ) + x = 95, или 19 x = 95 откуда x = 5.

Вместе с тем есть еще более интересный подход. Допустим, мы рассматриваем более короткий ряд чисел, например 3 + 4 + 5 + 6 + 7. Их сумма (25) при делении на 5 дает среднее, а именно 5, которое оказывается средним числом ряда. Для ряда в нашей задаче средним число является 10-й член, а поскольку целые числа последовательны, этот член является также средним арифметическим, или средним числового ряда из 19 членов. Таким образом, чтобы найти среднее, нужно просто взять сумму (95) и разделить ее на количество членов ряда (19). Ответ — 5. Эта упрощенная версия задачи позволяет представить исходное задание в значительно более простой форме и, таким образом, облегчить решение.