Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Участвовали в заплыве = 14;

Играли в баскетбол и ходили в поход = 8;

Участвовали в заплыве и играли в баскетбол = 3;

Играли в баскетбол = 13;

Участвовали в заплыве и ходили в поход = 5;

Ходили в поход = 16.

При сложении этих частей диаграммы Венна мы получаем 8 + 3 + 2 + 1 + 4 + 6 + 5 = 29. В лагере было 40 мальчиков, из которых 29 участвовали в спортивных мероприятиях, а 11 нет.

Сколько целых чисел, цифры которых расположены в порядке возрастания, находится между 4000 и 5000?

К решению этой задачи можно подойти, сообразив, что первой цифрой должна быть 4, а значит, на втором месте может стоять цифра 5, 6 или 7. Цифры 8 и 9 для этого не подходят, поскольку вслед за ними в возрастающем порядке уже ничего не расположишь. В результате таких рассуждений должно получиться следующее: 4567, 4568, 4569, 4578, 4579, 4589, 4678, 4679, 4689 и 4789.

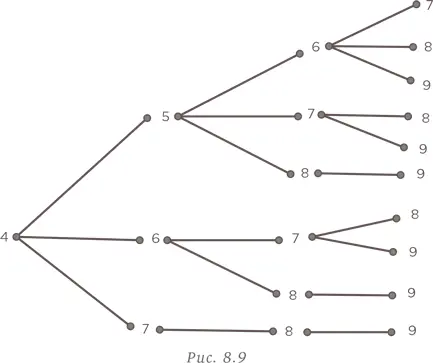
Чтобы подойти к решению более организованно, воспользуемся схемой, представленной на рис. 8.9, хотя задача по своему характеру не требует никаких рисунков.

Каждый путь, начинающийся от цифры 4, ведет к числу, которое находится в диапазоне между 4000 и 5000. Всего таких путей 10, и они дают следующие числа: 4567, 4568, 4569, 4578, 4579, 4589, 4678, 4679, 4689 и 4789. Таким образом, мы получаем искомые числа с помощью схемы, построения которой условия задачи не требуют.

У моего брата целая коллекция фигурок двуногих обезьян и четвероногих буйволов. Если в коллекции всего 100 фигурок и в сумме 260 ног, то сколько в ней фигурок каждого вида?

Чаще всего составляют два уравнения и решают их. Обозначим число фигурок обезьян как a , а число фигурок буйволов как b . Тогда мы получаем следующие уравнения:

a + b = 100;

2 a + 4 b = 260.

Умножение первого уравнения на 2 дает:

2 a + 2 b = 200;

2 a + 4 b = 260.

Если вычесть первое уравнение из второго, то мы получим:

2 b = 60;

b = 30.

Таким образом, в коллекции 30 буйволов и 70 обезьян.

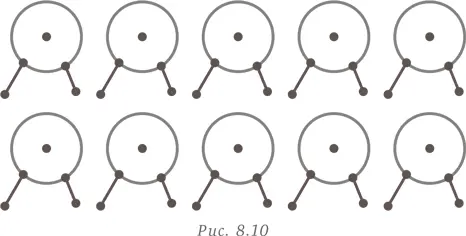
Воспользуемся визуальным представлением данных (нарисуем схему), чтобы решить задачу. Прежде всего, уменьшим числа в условиях задачи в 10 раз, чтобы ими было легче оперировать (но будем помнить о том, что полученный результат нужно умножить на 10 для восстановления исходного порядка чисел). Итак, теперь у нас всего 26 ног и 10 фигурок. Нарисуем 10 окружностей, которые будут представлять 10 фигурок. Независимо от того, что это за фигурка, обезьяна или буйвол, у нее должно быть не менее двух ног (рис. 8.10).

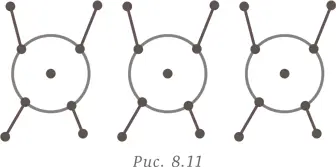
До нужной величины нам не хватает шести ног — их необходимо добавлять парами (рис. 8.11).

У нас получилось три четвероногих фигурки и семь двуногих. Осталось умножить их на 10. Таким образом, мы получаем 30 фигурок буйволов и 70 фигурок обезьян.

Мы знаем, что организация данных иногда очень облегчает поиск решения. Если нужно выявить, например, закономерность, то аккуратное представление данных в виде списка или таблицы может помочь в этом. Особенно интересны здесь исчерпывающие списки, т. е. списки, в которых систематизированно перечисляются все существующие возможности. В таких списках часто обнаруживается то, что мы ищем. Составление исчерпывающего списка позволяет тщательно проанализировать все возможности.

В качестве примера предположим, что у вас не работает лампа. Попробуем перечислить все возможности. (Конечно, это можно сделать мысленно, но в результате вы все равно получите список.) Проблема может крыться в перегоревшей лампочке, оборванном проводе, неработающей розетке, сработавшем предохранителе или неисправном выключателе. Проверяя возможности одну за другой, мы в конечном итоге дойдем до той, которая является причиной неисправности. Математический пример может выглядеть так:

Имеется двузначный квадрат целого числа. Если вставить одну цифру между существующими двумя, то получится трехзначный квадрат целого числа. Какие трехзначные квадраты чисел мы получаем?

Проанализируем все возможности. Прежде всего, составим исчерпывающий список двузначных квадратов целых чисел, их шесть:

16, 25, 36, 49, 64, 81.

Теперь составим исчерпывающий список трехзначных квадратов целых чисел:

100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961.

Выберем из второго списка те числа, которые можно составить, вставив какую-либо цифру между первой и второй цифрами двузначных квадратов целых чисел. Такому условию удовлетворяют только 196(вставлена 9 между цифрами числа 16), 225(вставлена 2 между цифрами числа 25) и 841(вставлена 4 между цифрами числа 81). Два исчерпывающих списка сделали очевидными все возможности. Обратите внимание на то, что исчерпывающий список не только содержит ответ задачи, но ограничивает количество исследуемых возможностей.

Вот еще один пример использования этой полезной стратегии.

На скамейке в парке сидят два человека. Один из них — женщина. Какова вероятность того, что и второй тоже окажется женщиной?

Составим список всех возможностей (М = мужчина, Ж = женщина):

М — М М — Ж Ж — М Ж — Ж.

В список пошли четыре возможности, однако в нашей задаче первую, М — М, не нужно учитывать, поскольку известно, что как минимум один человек — женщина. У нас остаются три варианта, и лишь в одном из них могут быть две женщины. Таким образом, ответом на поставленный вопрос будет вероятность, равная.

Чтобы еще лучше увидеть ценность такого подхода к решению задач, рассмотрим еще один пример:

В двух залах местного кинотеатра показывают по утрам разные мультфильмы. Утренние сеансы в обоих залах должны заканчиваться к 13:00, когда начинается демонстрация художественных фильмов. В зале A первый сеанс мультфильмов начинается в 9:00, второй в 9:28, а потом через каждые 28 минут. В зале B первый сеанс тоже начинается в 9:00, но потом сеансы повторяются через 35 минут. Джоанн хочет попасть на просмотр мультфильмов в обоих залах. Во сколько два последующих сеанса начинаются одновременно?

Составим исчерпывающий список времени начала сеансов в обоих залах.

Любой последующий сеанс должен был бы начаться уже после 13:00. Мы перечислили все возможности! Где-то в этом списке всех должен находиться ответ. Список показывает лишь одно время, когда начало сеансов в обоих залах совпадает — 11:20.