Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Ситуацию до и после перестановок можно представить схематично, или визуализировать ее:

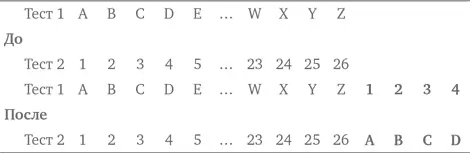
Теперь видно, что тесты содержат восемь одинаковых вопросов, а именно 1, 2, 3, 4 и A, B, C, D. Хотя в этом случае не обязательно использовать визуальное представление, и задачу можно решить другими методами, создание схемы позволяет увидеть , что происходит. Такой подход облегчает поиск решения. Имейте в виду, когда мы говорим о визуальном представлении, не обязательно подразумевается «вычерчивание» чего-либо.

Вот еще одна задача, где визуальное представление помогает увидеть происходящее.

Длина стороны равностороннего треугольника равна 40 см. Средние точки сторон соединяются так, что образуется второй равносторонний треугольник. Средние точки сторон этого треугольника соединяются так, что образуется третий треугольник. Этот процесс продолжается до тех пор, пока мы не получим пять треугольников. Чему равен периметр пятого треугольника?

Излишне говорить, что в случае решения геометрической задачи — даже такой, которую легко изложить на словах, — построение чертежа очень полезно, а то и просто необходимо. Нам нужно видеть, о чем идет речь (рис. 8.1).

Чертеж должен показывать, что отрезок, соединяющий средние точки двух сторон треугольника, равен половине длины третьей стороны и параллелен ей. Таким образом, каждая сторона любого нашего треугольника равна 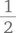длины соответствующей стороны предыдущего треугольника. Периметр каждого последующего треугольника равен половине периметра предыдущего треугольника. Для полной ясности составим таблицу, отражающую процесс.

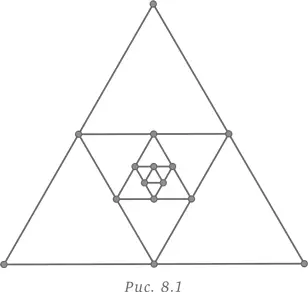
Периметр пятого треугольника равен 7,5 см. Сделанный нами чертеж помог визуализировать ситуацию и решить задачу. Хотя решить ее можно и без рисунка, глядя на чертеж, легче найти ответ.

Чтобы подчеркнуть ценность использования схематичного представления, когда это напрямую не требуется в условиях, рассмотрим такую задачу.

В 5:00 часы бьют пять раз в течение 5 секунд. Сколько времени потребуется этим часам, чтобы пробить 10 раз в 10:00? (Предполагается, что на сами удары часов время не требуется.)

Ответ 10 секунд неверен ! Характер этой задачи не предполагает создание каких-либо рисунков. Тем не менее представим ситуацию схематично, чтобы увидеть суть происходящего. На схеме каждая точка представляет удар часов. На рис. 8.2 мы видим, что общее время боя составляет 5 секунд, а между ударами четыре интервала.

Из этого следует, что интервал должен составлять 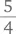секунды. Теперь рассмотрим второй случай на рис. 8.3.

Здесь мы видим, что между 10 ударами девять интервалов. Поскольку интервал равен 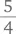секунды, продолжительность боя часов в 10:00 составит 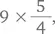или 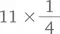секунды.

Схема значительно упростила задачу, которая иначе могла сбить человека с толку.

Стратегия составления схем или диаграмм, когда они не требуются по условиям задачи, нередко помогает найти решение, а в некоторых случаях прямо дает ответ, особенно в несложных задачах, где визуальное представление делает решение очевидным.

В классе г-на Страусса 25 столов, расставленных в виде квадрата в пять рядов по пять столов в каждом. Г-н Страусс хочет, чтобы все поменялись местами по такому правилу: каждый переходит за стол, находящийся слева или справа от него, или за стол, находящийся перед ним или позади него. Можно ли осуществить это?

Самый распространенный подход к решению этой задачи — взять 25 листочков бумаги, которые будут обозначать столы, и подвигать их в соответствии с правилом г-на Страусса. Это неудобно, в процессе трудно уследить за всеми перемещениями и получить правильный ответ.

Вместо того, чтобы двигать листочки, давайте сделаем схему, или визуально представим расположение столов. Изобразим класс с 25 столами в виде шахматной доски, как показано на рис. 8.4.

Чтобы ученики соблюдали правило г-на Страусса, им нужно переходить с закрашенного стола на незакрашенный или наоборот. Однако у нас 13 закрашенных столов и только 12 незакрашенных. Таким образом, пересаживание по правилу г-на Страусса невозможно.

Стоимость разрезания и сваривания звена цепи составляет $1,00. У женщины есть семь звеньев, и она хочет сделать из них цепь. Во сколько долларов как минимум это обойдется?

Наиболее очевидный подход — разрезать шесть звеньев, соединить их и сварить. Это будет стоить $6,00. Однако наверняка должен быть способ уменьшить затраты.

Воспользуемся стратегией визуального представления. Разомкнем звено 2 и соединим звенья 1, 2 и 3, как показано на рис. 8.5.

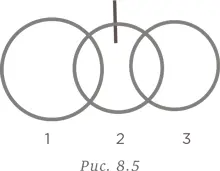
Разомкнем звено 5 и соединим звенья 4, 5 и 6, как показано на рис. 8.6.

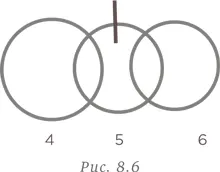
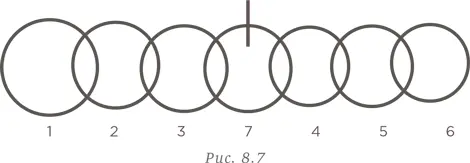
Наконец, разомкнем звено 7 и соединим цепочки 1–2–3 и 4–5–6, как показано на рис. 8.7.

Поскольку нам пришлось разрезать только три звена, создание цепи обойдется в $3,00.

Если в среднем полторы несушки могут снести полтора яйца за полтора дня, то сколько яиц снесут шесть несушек за восемь дней?

Это старая задача, которая выдержала испытание временем. Традиционно ее решают следующим образом. Поскольку 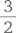несушки работают 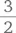дня, можно сказать, что работа по откладыванию полутора яиц 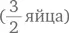занимает или 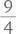«несушко-дня». Аналогичным образом вторая работа занимает 6 × 8, или 48 «несушко-дней». Таким образом, можно составить пропорцию.