Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Такая стратегия очень эффективна, но вы должны убедиться в том, что перечислили все без исключения возможности! Только тщательная организация данных может дать вам полную уверенность. Как и в случае с другими стратегиями, необходимо обдуманно подходить к выбору той, которая подходит в данном случае. Стратегия учета всех возможностей может сделать решение более очевидным.

Учитель математики замечает, что его нынешний возраст представляет собой простое число. Он обнаруживает, что в следующий раз его возраст станет простым числом через столько же лет, сколько прошло с той поры, когда возраст был простым числом в прошлый раз. Сколько лет учителю математики?

У этой задачи не так много альтернативных способов решения. Обычно начинают перебирать числа в надежде «наткнуться на подходящее».

Здесь наверняка нам пригодится стратегия учета всех возможностей. Рассмотрим следующий список:

В списке простых чисел от 1 до 100 (хотя в ситуации учителя математики можно было бы ограничиться числами в диапазоне от 20 до 80) только в двух случаях три последовательных простых числа имеют одинаковую разность. Первый случай — 3, 5 и 7 — нам не подходит, поскольку пятилетних учителей математики не бывает. Второй случай — 47, 53 и 59 — укладывается в подходящий возрастной диапазон. Таким образом, учителю математики должно быть 53 года.

Найдите количество сочетаний, при которых 20 монет достоинством 5 центов, 10 центов и 25 центов могут составить в сумме $3,10.

Большинство людей сразу начинают составлять алгебраические уравнения, отражающие информацию из условий задачи. В результате они получают: n + d + q = 20, где n, d и q — количество 5-, 10- и 25-центовых монет соответственно. Это можно записать, как n = 20 — q — d . Кроме того, 25 q + 10 d + 5 n = 310, что при объединении с предыдущими двумя уравнениями дает: 25 q + 10 d + 5 (20 — q — d ) = 310. Отсюда 4 q + d = 42, или 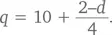После этого остается лишь подставлять разные значения, чтобы выявить наилучший результат.

У нас, однако, есть более рациональный метод, а именно учет всех возможных значений d . Прежде всего, мы замечаем, что q должно быть целым числом, а значит необходимо выделить дробную часть q , т. е. 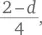или d = 2–4 k . Подставив это в приведенное выше уравнение, мы получаем q = 10 + k , а n = 20 — q — d = 20 — (10 + k ) — (2–4 k ), или n = 8 + 3 k .

Поскольку d = 2–4 k , значение k может быть либо нулевым, либо отрицательным.

В таблице ниже приведены возможные значения k и вытекающие из него значения d, q и n .

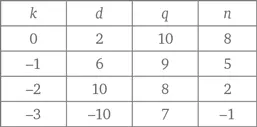
При k = 0, –1, –2 мы получаем реальные варианты. Когда же k = –3, d = 2–4(–3) = 14, а n = 8 + 3(–3) = –1, что не имеет смысла в этой задаче. Таким образом, количество сочетаний, при которых сумма составляет $3,10, равно трем.

Для доставки консервов из тунца компания может использовать небольшие коробки, в которые входит восемь банок, и коробки побольше, вмещающие 10 банок. С целью экономии компания старается чаще использовать большие коробки. Если заказ составляет 96 банок, то как лучше упаковать его для отправки?

Эта задача имеет любопытное математическое решение. Если обозначить как x количество небольших коробок, а как y количество больших коробок, то мы получим уравнение:

8 x + 10 y = 96.

В этом уравнении, однако, две неизвестные, что обычно означает наличие множества решений. Такое уравнение, где значения x и y могут быть только целыми, называют диофантовым по имени древнегреческого математика Диофанта (примерно 208–292 гг. н. э.). Попробуем решить его. Выразим x через y :

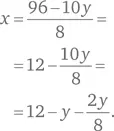
Значение члена 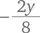должно быть целым, чтобы получить целое значение x . Пусть y = 4. Тогда 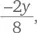а x = 12 − 4–1 = 7. Таким образом, мы получаем семь маленьких коробок и четыре больших. Могут ли существовать другие ответы? Попробуем поискать их. Аналогичным образом можно принять y = 0 и получить 12 и 0. Наконец при y = 8 мы получаем x = 2.

Для решения этой задачи лучше всего подходит стратегия учета всех возможностей и представление данных в табличной форме.

Похоже, мы сразу получили один правильный ответ! Он удовлетворяет численным условиям задачи — необходимо отправить 96 банок. Вместе с тем единственная ли это возможность? В конце концов, такой ответ означает, что компания не использует ни одной большой коробки. А из условий нам известно, что она стремится использовать максимальное количество больших коробок. Поэтому продолжим таблицу и попробуем найти все возможные варианты.

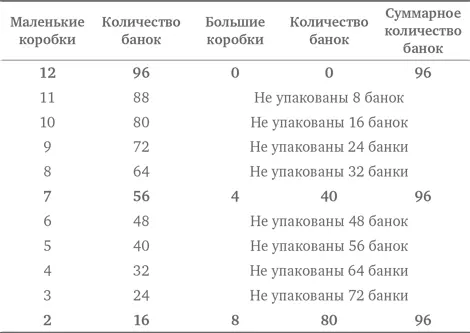
Существуют три варианта упаковки: 2 маленьких коробки и 8 больших; 7 маленьких коробок и 4 больших; 12 маленьких коробок и 0 больших. Вместе с тем, поскольку компания стремится использовать максимальное количество больших коробок, ответ для нашей задачи — 2 маленькие коробки и 8 больших. Обратите внимание на то, что с математической точки зрения все три ответа удовлетворяют условию, в соответствии с которым необходимо отправить 96 банок. Контекст задачи, однако, заставляет отбросить два варианта ответа из тех трех, что позволила выявить таблица.

На стандартном игральном кубике точки на противоположных гранях составляют в сумме 7. Сколько разных сумм дают точки на трех соседних гранях стандартного кубика?

Одни обычно пытаются нарисовать кубик и последовательно подсчитать точки на соседних гранях. Другие начинают выписывать возможные сочетания точек на трех гранях, независимо от того, находятся они рядом или нет.