Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам
- Название:Стратегии решения математических задач. Различные подходы к типовым задачам
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2018
- Город:Москва
- ISBN:978-5-9614-5172-6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам краткое содержание
В этой книге рассказывается о десяти различных стратегиях решения задач. Каждая глава начинается с описания конкретной стратегии и того, как ее можно использовать в бытовых ситуациях, а затем приводятся примеры применения такой стратегии в математике. Для каждой задачи авторы приводят сначала стандартное решение, а затем более элегантный и необычный метод. Так вы узнаете, насколько рассматриваемая стратегия облегчает поиск ответа.
Стратегии решения математических задач. Различные подходы к типовым задачам - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Обычный подход
Обычно начинают с составления уравнений. Возьмем за x количество рядов и колонок. Тогда первоначальное количество кустов равно x × x , или x 2. Обозначим дополнительные кусты в каждом ряду и колонке как b , тогда новое количество кустов будет равно ( x + b ) 2. Теперь у нас есть уравнение:
x 2+ 211 = ( x + b ) 2;
x 2+ 211 = x 2+ 2 bx + b 2;
211 = b 2+ 2 bx .
Здесь возникает проблема. Мы получили квадратное уравнение с неизвестной b , в котором есть еще одна неизвестная x . Что с ним делать? Возможно стоит подставить какие-нибудь значения вместо неизвестных и посмотреть, не удастся ли решить уравнение. Хотя такой подход и может дать правильный ответ, он не слишком эффективен.
Образцовое решение
Попробуем пойти путем выдвижения предположений и их проверки. Мы видим, что 211 — это простое число, а x и b должны быть целыми числами. Если разложить на множители приведенное выше уравнение, то мы получим:
211 = b ( b + 2 x ).
Поскольку 211 — это простое число, у него только два множителя: 211 и 1. Таким образом, b должно быть равным 1, а ( b + 2 x ) — 211. В результате мы получаем 2 x = 210, а x = 105. В одном ряду на старом поле было 105 кустов.
Задача 10.2
Джек хочет огородить прямоугольный участок, отведенный под огород. У него есть готовая ограда длиной 20 м. Какие размеры должен иметь участок, чтобы огороженная площадь была наибольшей?
Обычный подход
Наиболее очевиден алгебраический подход. Можно составить уравнения, а потом решить их. Обозначим длину, как x , а ширину, как y . Тогда мы получим:
2 x + 2 y = 20, или x + y = 10.
При составлении второго уравнения возникает проблема — как представить максимальную площадь? Иначе говоря, нам нужно получить xy = максимум. Что здесь можно сделать? Посмотрим, можно ли найти другой подход.
Образцовое решение
Первая же прикидка показывает, что, например, длина 8 и ширина 2 «подходят». Однако точно так же подходят и другие пары чисел. Воспользуемся стратегией обоснованного предположения и проверки, чтобы понять, какие размеры дают наибольшую площадь. Будем вести учет предположений в табличной форме. Поскольку для определения площади нужно умножить одну длину на одну ширину, ограничимся половиной периметра, равной 10. Начнем с наибольшей возможной длины.
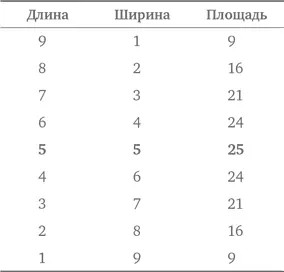
Похоже, что прямоугольник размером 5 × 5 (квадрат) имеет наибольшую площадь. А что, если попробовать дробные размеры? В условиях задачи не говорится, что они должны быть целыми. Добавим в нашу таблицу дробные значения и посмотрим, что произойдет.
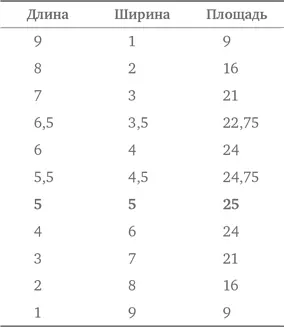
Все равно получается, что прямоугольник с периметром 20 м имеет наибольшую площадь при размерах 5 × 5 (квадрат). Некоторые и без этого знают, что при заданном периметре прямоугольника наибольшую площадь всегда имеет квадрат. А раз так, то ответ получается совсем быстро — это квадрат с периметром 20, площадь которого равна 5 × 5 = 25 м 2.
Задача 10.3
Найдите наименьшее простое число, превышающее 510. (Напомним, что простым называют такое число, которое делится только на 1 и на само себя.)
Обычный подход
Поскольку в задаче требуется найти наименьшее простое число, превышающее 510, мы будем, начиная с 511, брать число и пробовать разные делители в порядке возрастания вплоть до его половины. Если ни один из этих возможных делителей не подойдет, значит мы нашли простое число.
Образцовое решение
Воспользуемся стратегией обоснованного предположения и проверки для сужения диапазона возможных вариантов. Мы знаем, что число, превышающее 510, не может быть простым, если у него в конце стоят цифры 0, 2, 4, 5, 6 или 8. Кроме этого вспомним, что число, сумма цифр которого делится на 3, тоже делится на 3. Это позволяет отбросить некоторые числа, превышающие 510, например число 513. Таким образом, мы ограничиваем предположения числами 511, 517, 521 и т. д. В результате проверки следующим за 510 простым числом оказывается 521.
Задача 10.4
В эстафетном забеге на одну милю участвует команда в составе: Густав, Йохан, Ричард и Вольфганг. Они бегут свой четвертьмильный этап в том порядке, в котором перечислены. Каждый бегун проходит свой этап на 2 секунды быстрее предыдущего. Они финишируют с общим временем 3 минуты 40 секунд. За сколько каждый бегун пробежал свой этап?
Обычный подход
Применив несложные алгебраические вычисления, можно решить задачу следующим образом:
x = время, за которое свой этап пробежал Густав;
x — 2 = время, за которое свой этап пробежал Йохан;
x — 4 = время, за которое свой этап пробежал Ричард;
x — 6 = время, за которое свой этап пробежал Вольфганг.
x + ( x — 2) + ( x — 4) + ( x — 6) = 220
(3 минуты 40 секунд = 220 секунд);
4 x — 12 = 220;
4 x = 232;
x = 58.
Густав пробежал свой этап за 58 секунд, Йохан — за 56 секунд, Ричард — за 54 секунды, Вольфганг — за 52 секунды.
Образцовое решение
Конечно, это решение зависит от знания алгебраических методов. Вместе с тем задачу можно решить с помощью стратегии обоснованного предположения и проверки. Предположим, что бегуны прошли дистанцию примерно с одинаковой скоростью. Если так, то можно разделить 220 на 4 и получить 55 в качестве первого предположения.
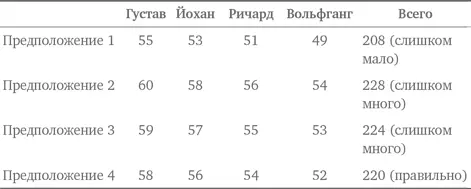
Таким образом, Густав пробежал свой этап за 58 секунд, Йохан — за 56 секунд, Ричард — за 54 секунды, Вольфганг — за 52 секунды.
Задача 10.5
В коробке у Дэна находятся почтовые марки стоимостью 13 и 8 центов. Отправка посылки, которую он приготовил, стоит ровно $1. Сколько марок каждого достоинства Дэн должен наклеить на посылку?
Обычный подход
Можно попробовать решить эту задачу алгебраически. Если обозначить как x количество 13-центовых марок и как y количество 8-центовых марок, то мы получим следующее уравнение:
0,13 x + 0,08 y = 1,00.
Если перевести все в центы, то уравнение приобретет вид:
13 x + 8 y = 100.
Это, однако, уравнение с двумя неизвестными, а значит ответов может быть несколько. Поскольку количество марок должно быть целым числом, нам нужно решить диофантово уравнение.
Для начала выразим y через x : 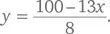 После деления и выделения целых величин и остаточных членов, а затем объединения остаточных членов мы получаем:
После деления и выделения целых величин и остаточных членов, а затем объединения остаточных членов мы получаем: 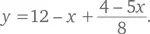
Интервал:
Закладка:










