Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Эту задачу можно решить алгебраически, составив шесть уравнений с шестью неизвестными:

B + C + D + E + F = 200;

A + C + D + E + F = 220;

A + B + D + E + F = 240;

A + B + C + E + F = 260;

A + B + C + D + F = 280;

A + B + C + D + E = 300.

Решение шести уравнений довольно трудоемко, поэтому попробуем поискать другой подход к этой задаче.

С помощью нашей стратегии организации данных можно упростить решение задачи и сделать его изящным. Начнем с представления данных в табличной форме:

Мы опять получили довольно громоздкий набор уравнений, но можно посмотреть на них с другой точки зрения и организовать данные вертикально, просуммировав колонки в вертикальном направлении:

5A + 5B + 5C + 5D + 5E + 5F = 1500.

Разделив обе стороны уравнения на 5, мы получаем:

A + B + C + D + E + F = 300.

Однако шестое взвешивание в таблице показывает, что A + B + C + D + E = 300 фунтам. Следовательно, ящик F должен весить 0 фунтов. Обратимся затем к пятому взвешиванию, которое показывает, что A + B + C + D + F = 280 фунтам. Однако мы уже знаем, что F = 0, а значит A + B + C + D = 280.

Вернемся к шестому взвешиванию — A + B + C + D + E = 300, вычтем из него последнее уравнение и получим E = 20фунтов.

Из четвертого взвешивания следует, что A + B + C + E + F = 260. Подставив в это уравнение уже известные значения F и E, мы получим A + B + C + 20 + 0 = 260, или A + B + C = 240. Подставляя это значение в пятое взвешивание, находим D = 40.

Если вычесть уравнение третьего взвешивания из уравнения четвертого взвешивания, то, зная, что F = 0, мы получаем:

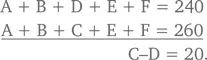
Поскольку D = 40, мы получаем C = 60.

Подставим известные значения в уравнение первого взвешивания: B + C + D + E + F = 200 = B + 60 + 40 + 20 + 0. Таким образом, B = 80.

Поступив аналогичным образом с уравнением второго взвешивания, получим A = 100.

Использование табличной формы сделало данные более понятными и позволило решить задачу путем логических рассуждений.

Даны трехзначные числа, которые составлены исключительно из нечетных цифр. Чему равна сумма всех этих чисел?

Обычно при решении задачи такого типа начинают составлять список нечетных чисел в том или ином порядке, а потом долго складывают их.

Главное здесь — организовать числа логичным образом. Например, наш список может выглядеть так: 111 + 113 + 115 + 117 + 119 + 133 + 135 + 137 + 139 + … + 511 + 513 + 515 + 517 + 519 + … + 991 + 993 + 995 + 997 + 999. Поскольку всего пять цифр могут находиться в каждом из трех разрядов, существует 5 × 5 × 5 = 125 возможных чисел. Если подойти к делу организованно, то можно складывать эти числа парами: первое и последнее, второе и предпоследнее и т. д. Сумма каждой из этих пар равна 1110. В нашем списке пар 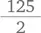чисел. Таким образом, сумма этих чисел составляет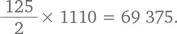

Данные можно организовать по-другому и также получить довольно изящное решение. Мы уже определили, что сложить нужно 125 целых чисел, каждое из которых состоит из трех цифр, а значит всего нам необходимо принять во внимание 375 цифр. Понятно, что каждое из пяти нечетных цифр — 1, 3, 5, 7 и 9 — встречается 75 раз, т. е. 25 раз в каждом разряде (в разряде сотен, десятков и единиц). Это можно представить в виде формулы следующим образом:

25 [100 (1 + 3 + 5 + 7 + 9) + 10 (1 + 3 + 5 + 7 + 9) + 1 (1 + 3 + 5 + 7 + 9)] = 25 × 25 × (100 + 10 + 1) = 69 375.

В каждом из приведенных примеров организации данных решение задачи становится значительно более изящным, чем в случае использования лобового метода.

Допустим, у нас есть 11 линий, лежащих в одной плоскости, при этом три линии проходят через точку P , а три линии имеют общую точку Q . Никакие другие три линии, кроме этих, не пересекаются. Чему равно минимальное количество точек пересечения этих 11 линий при таких условиях?

Чаще всего эту задачу пытаются решить методом проб и ошибок, но довольно большое количество линий (11) делает такой подход проблематичным. Таким образом, должен быть какой-то другой, более эффективный способ решения подобной задачи.

Чтобы решить такую задачу, нужно организовать линии логичным образом. Начнем с построения трех линий, пересекающихся в точке P , как показано на рис. 7.6.

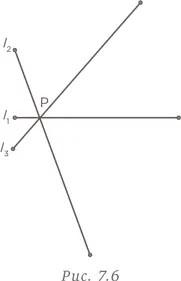
Повторим эту процедуру с точкой Q , построив линии l 3||l 4 и l 2||l 5 , как показано на рис. 7.7.

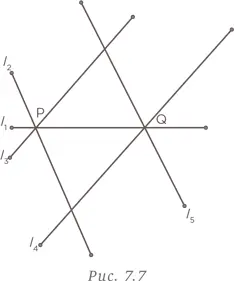
Затем проведем шесть оставшихся линий параллельно линии l 2 . Это показано на рис. 7.8. Каждая из этих линий добавляет три новые точки пересечения.

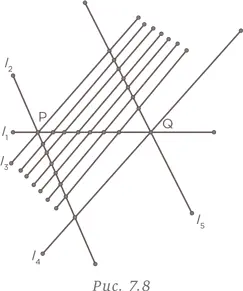
Таким образом, в результате организации исходных данных логичным образом мы получаем следующее количество точек пересечения: 6 × 3 + 4 = 22.

Если напечатать все числа от 1 до 1 000 000, сколько раз в них встретится цифра 8?

Обычно в ответ на такой вопрос, который кажется ошеломляющим, начинают составлять список чисел без какого-либо намека на их организацию. При таком подходе решение зависит от того, удастся ли увидеть какую-нибудь закономерность в числовом ряду.

Лучшая стратегия здесь заключается, пожалуй, в организации данных таким образом, чтобы можно было выявить любую закономерность в списке, если она существует.

В представленных выше шести разрядах миллиона цифры 0, 1, 2, 3, 4, …, 8 и 9 используются равное количество раз. Это понятно потому, что каждую «комбинацию» можно составить из каждой из 10 цифр. Таким образом, цифра 8 должна появиться в 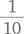случаев, или 600 000 раз.

У продавца двое часов, которые бьют полночь одновременно. Однако одни часы спешат на 1 минуту в час, а другие отстают на 1 минуту в час. Если такая разница сохранится и дальше, то через какое время их показания совпадут?