Авинаш Диксит - Стратегические игры

c) Профсоюз рабочих автомобильной промышленности США хотел бы, чтобы правительство США ограничило импорт автомобилей.

Упражнения без решений

U1.В одном из эпизодов фильма Manhattan Murder Mystery («Загадочное убийство в Манхэттене») герои Вуди Аллена и Дайан Китон находятся на хоккейном матче в Madison Square Garden. Героиня явно чувствует себя не в своей тарелке, но спутник говорит ей: «Не забывай о нашей сделке. Ты остаешься со мной до окончания матча, а на следующей неделе я иду с тобой в оперу и пробуду там до конца». Позже мы видим, как они выходят из театра Metropolitan Opera на безлюдную площадь Линкольн-центра, тогда как в театре все еще играет музыка. Героиня Китон расстроена: «Как же насчет сделки? Я посмотрела с тобой весь хоккейный матч, а ты обещал до конца оставаться в опере». Герой Аллена отвечает: «Видишь ли, я не могу долго слушать Вагнера. В конце первого акта я уже почувствовал желание захватить Польшу». На основании знаний теории стратегических ходов и обеспечения их достоверности прокомментируйте стратегический выбор, сделанный участниками этой игры.

U2.Рассмотрим игру между одним из родителей и ребенком. Ребенок может вести себя хорошо (Х) или плохо (П); родитель может наказать ребенка (Н) или воздержаться от наказания (В). Ребенок получает от плохого поведения удовольствие, имеющее для него ценность 1, но наказание наносит ему эмоциональную травму, ценность которой −2. Таким образом, если ребенок ведет себя хорошо и его не наказывают, он выигрывает 0, а если плохо и его наказывают, то 1 − 2 = −1 и т. д. Родитель получает выигрыш −2 от плохого поведения ребенка и −1, когда наказывает ребенка.

a) Сформулируйте эту игру как игру с одновременными ходами и найдите равновесие Нэша.

b) Предположим, сначала ребенок выбирает стратегию «хорошее поведение» или «плохое поведение», после чего родитель, исходя из выбора ребенка, применяет стратегию «наказать» или «воздержаться от наказания». Нарисуйте дерево игры и найдите совершенное равновесие подыгры.

c) Теперь допустим, что прежде чем ребенок начнет действовать, родитель берет на себя обязательство совершить определенный ход — например, применяет угрозу «Н, если П» («Если будешь вести себя плохо, я тебя накажу»). Сколько таких стратегий есть у родителя? Составьте таблицу этой игры. Найдите все равновесия Нэша в чистых стратегиях.

d) Чем отличаются ваши ответы в пунктах b и c? Объясните причину такого различия.

U3.Профессор Уильям Шаррон из Сент-Луисского университета описал общую стратегическую игру, представленную в труде Фукидида о Пелопоннесской войне, в терминах теории игр [158]. Афины создали большую империю, в которую вошли города на побережье Эгейского моря, воспользовавшись своей ролью лидера по защите греческих государств от персидских завоевателей. Спарта, опасаясь афинского влияния, замыслила войну против Афин. Но если бы Спарта решила ее не начинать, Афинам пришлось бы решать, сохранять свою власть в империи или отказаться от нее. К тому же Афины опасались, что, получив независимость, города могут присоединиться к Спарте и образовать более мощный союз против Афин, за что Спарта предоставила бы им весьма выгодные условия. Таким образом, в игре есть три игрока — Спарта, Афины и малые города; игроки делают ходы именно в таком порядке. В этой игре существует четыре исхода с выигрышами, представленными в следующей таблице (4 — самый высокий выигрыш):

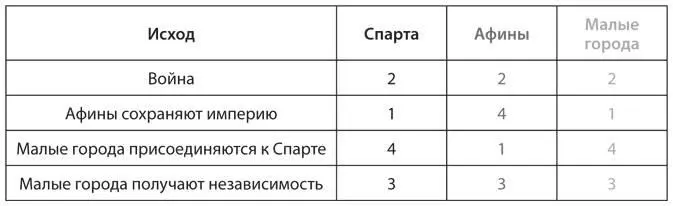
a) Нарисуйте дерево игры и найдите равновесие обратных рассуждений. Есть ли в этой игре исход, более благоприятный для всех игроков?

b) Какой стратегический ход или ходы могли бы обеспечить более благоприятный исход? Проанализируйте достоверность таких ходов.

U4.Конфигурацию выигрышей в игре из упражнения S3можно изменить так, чтобы сказанное в объявлении детей представляло собой угрозу, а не обещание.

a) Нарисуйте новое дерево игры из пункта а упражнения S3и запишите выигрыши обоих игроков таким образом, чтобы объявление детей стало угрозой в сугубо формальном смысле.

b) Найдите в игре статус-кво, а также определите, будет ли угроза сдерживающей или принуждающей.

c) Объясните, почему достоверность этой угрозы не подтверждается автоматически, с учетом вашей структуры выигрышей.

d) Объясните, почему достоверность подразумеваемого обещания подтверждается автоматически.

e) Объясните, почему дети больше всего хотели бы выдвинуть угрозу, и предложите способ, позволяющий сделать ее достоверной.

U5.Ответьте на вопросы, сформулированные в упражнении S5, в контексте следующих ситуаций.

a) Студенты вашего университета или колледжа хотят помешать администрации повысить плату за обучение.

b) Большинство участников конфликтов, так же как и другие страны, хотят добиться прочного мира в Афганистане, Ираке, Израиле и Палестине.

c) Почти все страны мира хотят, чтобы Иран закрыл свою ядерную программу.

U6.Составьте краткое описание игры с вашим участием, в которой были сделаны такие стратегические ходы, как обязательство, угроза или обещание; уделите особое внимание важному аспекту этих ходов, а именно достоверности. По возможности проиллюстрируйте игру и объясните, почему она закончилась именно так, а не иначе. Опирались ли игроки на глубокое стратегическое мышление при принятии решений?

В этой главе мы продолжим изучать широкий класс игр и остановимся на концепции «дилемма заключенных». Пожалуй, это классический пример теории стратегии и ее последствий для прогнозирования поведения участников игры, и большинство людей, изучающих теорию игр, с ним знакомы. Даже те, кто не имеет никаких знаний в данной области, наверняка наслышан об этой концепции или как минимум о ее существовании. Дилемма заключенных — это игра, в которой у каждого игрока есть доминирующая стратегия, но равновесие, возникающее в результате применения всеми игроками своих доминирующих стратегий, обеспечивает каждому из них худший исход, чем при использовании доминируемых стратегий. Парадоксальность этого равновесия поднимает ряд более сложных вопросов о характере взаимодействия участников игры, ответить на которые можно только посредством тщательного анализа. Цель данной главы — предоставить вам дополнительные инструменты такого анализа.

В разделе 3 главы 4мы уже сталкивались с дилеммой заключенных. Там же мы обратили внимание на любопытную природу равновесия, которое на самом деле «плохой» исход для игроков. «Заключенные» могут найти другой исход, более предпочтительный равновесному, но у них возникают трудности с выполнением этой задачи. В данной главе мы рассмотрим вероятность достижения такого исхода. Иными словами, проанализируем, могут ли (и каким образом) участники игры «дилемма заключенных» достичь и сохранить взаимовыгодный кооперативный исход, преодолев свою естественную заинтересованность в отказе от сотрудничества ради личной выгоды. Сначала разберем стандартную игру «дилемма заключенных», а затем сформулируем три категории решений. Первый и самый важный метод решения таких игр сводится к повторению стандартной однократной игры. Именно за разработку общей теории повторяющихся игр Роберт Ауманн (вместе с Томасом Шеллингом) в 2005 году получил Нобелевскую премию по экономике. Как обычно, на вводном этапе мы приведем несколько простых примеров этой общей теории, а затем проанализируем еще две категории возможных решений, в основе которых лежат схемы взыскания (или вознаграждения) и роль лидерства.