Авинаш Диксит - Стратегические игры

S4.Вам необходимо решить, стоит ли инвестировать 100 долларов в предприятие друга, где через год эта сумма вырастет до 130 долларов. Вы с другом договорились, что он вернет вам 120 долларов, оставив 10 долларов себе. Но не исключено, что ваш друг может сбежать со всей суммой (130 долларов). Деньги, которые вы не инвестируете в предприятие друга, можно безопасно вложить куда-то еще под действующую ставку процента r и получить 100(1 + r ) долларов в следующем году.

a) Постройте дерево игры для такой ситуации и покажите равновесие обратных рассуждений.

Теперь допустим, что игра повторяется бесконечное количество раз. То есть каждый год у вас есть возможность вложить еще 100 долларов в предприятие друга, и вы делите затем полученные 130 долларов по оговоренной выше схеме. Начиная со второго года вам предстоит принимать решение о целесообразности дальнейших инвестиций в предприятие друга, исходя из того, вернул он вам деньги за предыдущий год или нет. Процентная ставка между любыми двумя периодами подряд равна r — столько же, сколько и рыночная процентная ставка, и одинакова для вас и вашего друга.

b) При каких значениях r возможен равновесный исход в повторяющейся игре, в которой на протяжении каждого периода вы вкладываете деньги в предприятие друга и он выплачивает вам деньги в соответствии с договоренностью?

c) Если процентная ставка составляет 10 % в год, существует ли альтернативная договоренность о разделении прибыли, представляющая собой равновесный исход бесконечно повторяющейся игры, в которой в каждом периоде вы инвестируете средства в предприятие друга и он выплачивает вам деньги в соответствии с договоренностью?

S5.Вернитесь к примеру из упражнения S3, в котором заработная плата менеджеров двух подразделений компании зависит от выбора ими высокого или низкого уровня усилий, которые они вкладывают в работу. В пункте b этого упражнениясказано, что издержки в связи с выбором высокого уровня усилий составляют 60 000 долларов. Теперь допустим, что оба менеджера многократно ведут игру, представленную в пункте b упражнения S3, на протяжении многих лет. Такое повторение делает возможным особый тип сотрудничества, при котором один из менеджеров выбирает высокий уровень усилий, тогда как другой — низкий. При этом оба заключают соглашение о сотрудничестве, в соответствии с которым менеджер, выбирающий высокий уровень усилий, выплачивает второму менеджеру дополнительные суммы с тем, чтобы оба получили одинаковые выигрыши.

a) Какой размер дополнительного платежа гарантирует, что окончательные выигрыши двух менеджеров будут одинаковыми? Сколько каждый менеджер заработает за тот год, в течение которого будет действовать соглашение о сотрудничестве?

b) Сотрудничество в этой повторяющейся игре подразумевает выбор каждым менеджером предписанного уровня усилий и соответствующие дополнительные платежи менеджера с высоким уровнем менеджеру с низким. При каких значениях процентной ставки такое соглашение может поддерживать между ними сотрудничество в повторяющейся игре?

S6.Рассмотрим игру в труса, о которой шла речь в главе 4, с несколько более общими выигрышами (на рис. 4.13 k = 1).

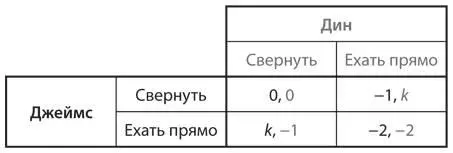
Предположим, это повторяющаяся игра, которая проводится каждую субботу вечером. Если k < 1, двум игрокам выгодно постоянно взаимодействовать, выбирая стратегии «свернуть» / «свернуть», тогда как при k > 1 им выгодно сотрудничать в случае, если один их них применит стратегию «свернуть», а другой — «ехать прямо», каждую неделю по очереди выбирая стратегию «ехать прямо». Может ли любой из этих двух типов сотрудничества быть устойчивым?

S7.Вспомните игру из упражнения S8в главе 5, где Южная Корея и Япония конкурируют на рынке производства танкеров класса VLCC. Как и в пунктах а и b этого упражнения, стоимость строительства судов составляет 30 миллионов долларов в каждой стране, а спрос на танкеры равен P = 180 — Q , где Q = q Корея + q Япония.

a) Ранее мы нашли равновесие Нэша в этой игре. Теперь найдите исход, основанный на сговоре. Какое общее количество танкеров должны производить обе страны, чтобы максимизировать свою прибыль?

b) Предположим, две страны выпускают одинаковое количество танкеров класса VLCC, а значит, имеют равную долю в прибыли, полученной в случае сговора. Какую прибыль получит каждая страна? Сравните ее с прибылью, которую бы они имели в случае равновесия Нэша.

c) Теперь давайте допустим, что две страны поддерживают повторяющееся взаимодействие. Один раз в год они определяют объем производства, и каждая страна располагает информацией о том, сколько танкеров выпустил конкурент за прошлый год. Обе страны хотят сотрудничать ради получения прибыли, вычисленной в пункте b. На протяжении любого отдельно взятого года каждая из стран может нарушить условия соглашения. Если одна из них сохранит количество выпущенных танкеров на оговоренном уровне, какое количество танкеров лучше всего построить другой стране? Какую прибыль в итоге получат они обе?

d) Составьте матрицу выигрышей этой игры, представив ее в виде дилеммы заключенных.

e) При каких значениях процентной ставки возможно поддержание сговора в случае, если две страны используют стратегию бесповоротного наказания, которая сводится к отказу от сотрудничества навсегда?

U1.Два человека, Бейкер и Катлер, играют в игру, в которой выбирают и делят приз. Бейкер решает, каким будет общий размер приза, 10 или 100 долларов. Катлер выбирает, как разделить приз, выбранный Бейкером: либо поровну, либо в неравных частях; тогда он получит 90 процентов, а Бейкер 10. Составьте таблицу выигрышей в этой игре и найдите ее равновесия для каждой из следующих ситуаций.

a) Ходы делаются одновременно.

b) Бейкер ходит первым.

c) Катлер ходит первым.

d) Является ли эта игра дилеммой заключенных? Почему да или почему нет?

U2.Рассмотрим небольшой городок, жители которого очень любят пиццу, но в нем можно разместить только две пиццерии, Deep Dish Донны и Pizza Pies Пирса. Каждый торговец должен выбрать цену на свою пиццу, но для простоты предположим, что доступны только две цены: высокая и низкая. При высокой цене торговцы могут получить прибыль 12 долларов на одну пиццу, при низкой — 10 долларов. У каждой пиццерии есть круг лояльных клиентов, которые покупают 3000 штук пиццы в неделю независимо от назначенной пиццерией цены. Существует также плавающий спрос в размере 4000 пицц в неделю. Но их покупатели чувствительны к ценам и пойдут в заведение с более низкой ценой. Если обе пиццерии установят одинаковую цену, они разделят этот спрос пополам.