Авинаш Диксит - Стратегические игры

b) Если компании поддерживают сотрудничество и выбирают общую наилучшую цену P , то прибыль каждой компании составит:

Y Донна = Y Пирс = ( P — 3)(12 — P + 0,5 P ) = ( P — 3)(12 — 0,5 P ).

Какую цену выберут компании, чтобы максимизировать общую прибыль?

c) Представим, что две пиццерии поддерживают повторяющееся взаимодействие, пытаясь сохранить рассчитанные в пункте b общие цены, максимизирующие прибыль. Они печатают новое меню каждый месяц, тем самым связывая себя обязательствами на весь этот период. На протяжении любого месяца одна из компаний может отказаться от этих обязательств. Если одна пиццерия сохранит цену на согласованном уровне, при какой цене другой выгоднее отказаться от дальнейшего сотрудничества? Какую прибыль получат обе пиццерии в итоге? При каких значениях процентной ставки сговор между ними будет устойчивым благодаря стратегии бесповоротного наказания?

U7.Давайте расширим анализ, представленный в упражнении S7, допустив возможность отказа от сотрудничества в триополии, построенной на сговоре. В упражнении S9в главе 5мы нашли основанный на равновесии Нэша исход игры в случае триополии на рынке производства танкеров класса VLCC, в состав которой входят Корея, Япония и Китай.

a) Теперь найдите исход этой игры, основанный на сговоре. То есть определите, какое количество танкеров VLCC должны выпускать три страны, чтобы обеспечить максимальную общую прибыль.

b) Предположим, в случае построенного на сговоре исхода игры, найденного в пункте а, эти три страны производят равное количество танкеров VLCC, а значит, каждая из них получает равную долю в общей прибыли. Какой будет прибыль каждой страны? Сравните ее с объемом прибыли, которую получит каждая страна в случае равновесия Нэша.

c) Теперь представим, что эти страны поддерживают повторяющееся взаимодействие. Один раз в год они определяют объем производства, причем каждая страна знает, сколько танкеров выпустили конкуренты в предыдущем году. Эти страны хотят сотрудничать, чтобы получать основанные на сговоре уровни прибыли, рассчитанные в пункте b. На протяжении любого года одна из стран может нарушить соглашение. Если две другие страны, как предполагается, должны обеспечить свою долю предусмотренного сговором результата, вычисленного в пунктах а и b, то какое количество танкеров лучше всего построить стране, отказавшейся от дальнейшего сотрудничества? Какую прибыль она в итоге получит, если выпустит оптимальное количество танкеров, тогда как две другие страны произведут столько, сколько было оговорено?

d) Безусловно, через год после отказа одной из стран от дальнейшего сотрудничества оба ее конкурента также его прекратят. Все три страны вернутся к исходу, основанному на равновесии Нэша (навсегда, в случае применения стратегии бесповоротного наказания). Какой выигрыш получит страна, переставшая сотрудничать с конкурентами, за один год отказа от основанного на сговоре исхода? Какие убытки понесет за каждый последующий год страна, отказавшаяся от сотрудничества, в связи с получением прибыли согласно равновесию Нэша, вместо прибыли, предусмотренной сговором?

e) При каких значениях процентной ставки сговор между тремя странами будет устойчивым благодаря стратегии бесповоротного наказания? Они выше или ниже значений, найденных в случае дуополии в пункте e упражнения S7? Почему?

Для вычисления приведенной стоимости необходимо определить текущую стоимость суммы денег, которая будет получена в будущем. Как мы видели в разделе 2, приведенная стоимость суммы денег (скажем, суммы x ), которая будет получена через n месяцев начиная с текущего момента, рассчитывается по формуле x / 1 + r ) n , где r — соответствующая месячная норма прибыли. Однако суммарную приведенную стоимость суммы денег, которая будет получена в следующем месяце и в каждом последующем месяце в обозримом будущем, определить труднее. В этом случае платежи делаются на протяжении неопределенного периода, а значит, не существует заданного предела суммы значений приведенной стоимости, которую необходимо определить. Для того чтобы вычислить текущую стоимость такого потока платежей, нужно знать математические правила суммирования бесконечных рядов.

Рассмотрим игрока, который в текущем месяце получит прибыль 36 долларов за счет отказа от сотрудничества, а затем ежемесячно будет терять по 36 долларов в связи с дальнейшим выбором этой стратегии, за что соперник будет его наказывать (применяя стратегию равноценных ответных действий). За первый из будущих месяцев (первый месяц, на протяжении которого игрок понесет убытки и за который необходимо дисконтировать значения стоимости) приведенная стоимость убытка игрока составит 36/(1 + r ); за второй будущий месяц — 36/(1 + r ) 2; за третий месяц — 36/(1 + r ) 3. Иными словами, за каждый из n будущих месяцев, на протяжении которых игрок будет нести убытки в связи с отказом от сотрудничества, его убыток составит 36/(1 + r ) n .

Общую приведенную стоимость всех будущих убытков этого игрока можно записать в виде суммы с бесконечным количеством членов ряда

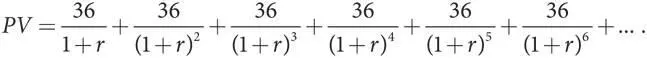
Эту же сумму можно записать с помощью специального обозначения со знаком суммы

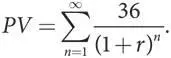
Это выражение эквивалентно предыдущему и читается так: «Сумма от n равно 1 до n равно бесконечности дробей с 36 в числителе и (1 + r ) в n -й степени в знаменателе». Поскольку 36 — это общий множитель (он присутствует во всех членах суммы), его можно вынести за знак суммы. Поэтому текущую стоимость можно записать так:

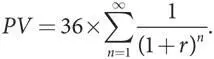
Теперь, чтобы вычислить фактическую приведенную стоимость, нам необходимо найти значение суммы, которая содержится в этом выражении для приведенной стоимости. Для этого упростим запись, подставив коэффициент дисконтирования δ вместо 1/(1 + r ). Тогда сумма, оценка которой нас интересует, равна

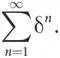
Здесь важно отметить, что 1/(1 + r ) < 1, поскольку значение r строго положительное.

Взглянув на последнюю сумму, специалист по бесконечным суммам [179]сказал бы, что она сходится к конечной величине δ/(1 + δ). Такая сходимость обеспечивается за счет того, что все большие степени числа, меньшего 1 (в данном случае δ), становятся все меньше и меньше, приближаясь к нулю по мере стремления n к бесконечности. При этом последние члены выражения, описывающего приведенную стоимость, уменьшаются до тех пор, пока не станут настолько маленькими, что весь ряд приблизится к определенному значению суммы, но сугубо формально никогда его не достигнет. Для того чтобы сделать вывод о том, что сходящееся значение суммы составляет δ/(1 + δ), понадобятся более сложные математические выкладки. Тем не менее достаточно просто доказать, что это правильный ответ.