Авинаш Диксит - Стратегические игры

a) Составьте таблицу выигрышей для этой игры в ценообразование между пиццериями, воспользовавшись прибылью каждой пиццерии за неделю (в тысячах долларов). Найдите в игре равновесие Нэша и объясните, почему это дилемма заключенных.

b) Теперь предположим, что у Deep Dish Донны гораздо больше лояльных клиентов, которые гарантированно покупают 11 000 (а не 3000) пицц в неделю. Размер прибыли и уровень плавающего спроса остаются теми же. Составьте таблицу выигрышей в новой версии игры и найдите равновесие Нэша.

c) Как наличие более крупной базы лояльных клиентов у Deep Dish «решает» дилемму, возникшую у этих двух пиццерий?

U3.Городской совет состоит из трех членов, которые ежегодно голосуют за повышение собственной заработной платы. Для принятия такого решения требуются два голоса «за». Каждый член совета хотел бы повышения, но при этом ему выгоднее голосовать против, поскольку это бонус в глазах избирателей. Выигрыши каждого члена городского совета таковы:

решение о повышении принято, свой голос «против»: 10;

решение о повышении не принято, свой голос «против»: 5;

решение о повышении принято, свой голос «за»: 4;

решение о повышении не принято, свой голос «за»: 0.

Все три члена городского совета голосуют одновременно. Составьте трехмерную таблицу выигрышей и покажите, что в случае равновесия Нэша решение о повышении заработной платы не может быть единогласным. Проанализируйте, как повторяющееся взаимодействие между членами совета может обеспечивать им ежегодное повышение заработной платы, если 1) каждый член совета занимает эту должность на протяжении трех лет; 2) каждый год в рамках ротации один из них должен быть переизбран; 3) у горожан короткая память, поэтому они помнят результаты голосования о повышении заработной платы членов городского совета только за прошлый, но не за предыдущие годы.

U4.Рассмотрим игру, которую проводит нейтральный судья, разработанную Джеймсом Андреони и Хэлом Вэрианом из Мичиганского университета [178]. В ней участвуют два игрока — Строка и Столбец. Судья дает каждому из них две карточки: 2 и 7 Строке и 4 и 8 Столбцу. Эта информация доступна всем участникам игры. Затем игрокам, играющим одновременно и независимо друг от друга, предлагают отдать судье карточку либо с б о льшим, либо с меньшим числом. Судья раздает выигрыши в долларах (взятых из общего фонда, а не из кармана игроков), размер которых зависит от того, какие карточки он собирает. Если Строка выберет карточку с меньшим числом 2, ее выигрыш составит 2 доллара; если Строка отдаст карточку с б о льшим числом 7, тогда Столбец получит 7 долларов. Если Столбец отдаст карточку с меньшим числом 4, то он получает 4 доллара; если Столбец выберет карточку с б о льшим числом 8, то Строка получит 8 долларов. Выигрыши от других вариантов сочетаний карточек показаны в таблице выигрышей.

a) Покажите, что полная таблица выигрышей в этой игре выглядит следующим образом.

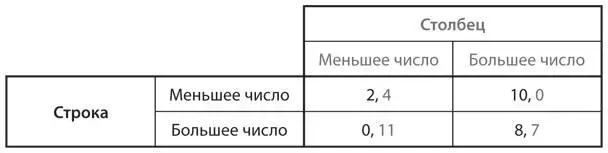
b) Найдите равновесие Нэша в этой игре. Определите, будет ли она дилеммой заключенных.

Теперь предположим, что игра состоит из следующих этапов. Судья раздает карточки, как и раньше, и информация о них известна всем. На этапе 1 каждый игрок из собственного кармана может выделить определенную сумму, которая будет храниться у судьи на счете условного депонирования; сумма может быть нулевой, но не отрицательной. Когда оба игрока сделают выбор на этапе 1, эта информация обнародуется. Далее на этапе 2 оба игрока снова выбирают карточки одновременно и независимо друг от друга. Судья раздает выигрыши из общего фонда, как и в случае одноэтапной игры. Кроме того, он распоряжается средствами, находящимися на счете условного депонирования, следующим образом. Если Столбец выберет карточку с б о льшим числом, судья отдаст ему сумму, которую дала на хранение Строка; если Столбец выберет карточку с меньшим значением, выделенная Строкой сумма вернется к ней. Сумма, которую внес на счет условного депонирования Столбец, распределяется по аналогичному принципу, в зависимости от того, какую карточку выберет Строка. Эти правила известны всем участникам игры.

c) Найдите равновесие обратных рассуждений (совершенное равновесие подыгры) в этой двухэтапной игре. Решает ли оно дилемму заключенных? Какова роль счета условного депонирования?

U5.Компании Glassworks и Clearsmooth конкурируют на местном рынке ремонта ветровых стекол. Размер рынка (общий объем прибыли этих компаний) составляет 10 миллионов долларов в год. Каждая компания решает, размещать ли ей рекламу на местном телевидении. Если компания решит размещать рекламу в том или ином году, это обойдется ей в 3 миллиона долларов. Если одна компания разместит рекламу, а другая нет, то первая захватит весь рынок. Если рекламу разместят обе компании, они поделят рынок поровну. Если обе решат не размещать рекламу, они также поделят рынок поровну.

a) Допустим, обе компании знают, что будут конкурировать всего один год. Составьте матрицу выигрышей в этой игре. Найдите стратегии, образующие равновесие Нэша.

b) Предположим, компании играют в эту игру пять лет подряд и знают, что к концу пятилетнего периода обе планируют выйти из бизнеса. Найдите совершенное равновесие подыгры в этой игре из пяти периодов. Обоснуйте свой ответ.

c) В чем состояла бы стратегия «око за око» в игре, описанной в пункте b?

d) Представим, что компании будут играть в эту игру неопределенное время и что их будущая прибыль дисконтируется по ставке 20 % в год. Можете ли вы найти совершенное равновесие подыгры, обеспечивающее более высокие годовые выигрыши, чем равновесие, найденное в пункте b? Если да, объясните, какие стратегии в него входят. Если нет, обоснуйте свой вывод.

U6.Вернитесь к пиццериям Deep Dish Донны и Pizza Pies Пирса, о которых шла речь в упражнении U2. Предположим, они не ограничены выбором из двух возможных цен и могут выбрать конкретное значение цены, обеспечивающей максимальную прибыль. Допустим также, что приготовление одной пиццы обходится в 3 доллара (в каждой пиццерии), а опыт или результаты изучения рынка показали наличие такой зависимости между объемом продаж ( Q ) и ценой ( P ):

Q Пирс = 12 — P Пирс + 0,5 P Донна.

Тогда прибыль каждой компании за неделю ( Y , в тысячах долларов) составит:

Y Пирс = ( P Пирс — 3) Q Пирс = ( P Пирс — 3)(12 — P Пирс + 0,5 P Донна),

Y Донна = ( P Донна — 3) Q Донна = ( P Донна — 3)(12 — P Донна + 0,5 P Пирс).

a) С помощью этих функций прибыли определите правило наилучших ответов каждой компании, как показано в главе 5, и используйте эти правила для поиска равновесия Нэша в данной игре. Какие цены выберут компании в случае равновесия? Какую прибыль получит каждая компания за неделю?