Авинаш Диксит - Стратегические игры

Чтобы доказать истинность нашего утверждения, мы используем один простой прием. Возьмем сумму первых m членов ряда и обозначим ее как S m . Таким образом получим

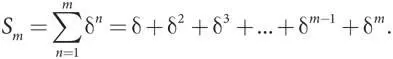
Теперь умножим эту сумму на (1 — δ), чтобы получить следующее выражение: (1 — δ) S m = δ + δ 2 + δ 3 + … + δ m — 1 + δ m — δ 2 — δ 3 — δ 4 — … — δ m — δ m + 1 = δ — δ m + 1.

Разделив обе стороны на (1 — δ), имеем

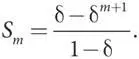
И наконец, возьмем предел этой суммы в случае приближения m к бесконечности, чтобы определить значение исходной бесконечной суммы. По мере стремления m к бесконечности значение δ m +1приближается к нулю, поскольку очень большие и увеличивающиеся степени числа, меньшего 1, становятся все меньше, но остаются неотрицательными. Таким образом, когда m стремится к бесконечности, правая сторона представленного выше уравнения приближается к δ / (1 — δ), а значит, это и есть предел S m , когда m стремится к бесконечности. Что и требовалось доказать.

Для того чтобы использовать полученный ответ для вычисления значений текущей стоимости в играх с дилеммой заключенных, необходимо восстановить значение r . Поскольку δ = 1/(1 + r ), из этого следует, что

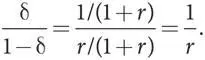
В таком случае текущая стоимость бесконечного потока убытков в размере 36 долларов, понесенных в каждом месяце, начиная со следующего, составляет

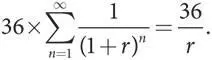
Это и есть значение, использованное нами для определения того, стоит ли игроку навсегда отказываться от сотрудничества, в разделе 2. Обратите внимание, что введение вероятности продолжения p ≤ 1 в вычисление дисконтированных значений ничего не меняет в примененной здесь процедуре суммирования. В представленных выше вычислениях мы вполне могли бы подставить R вместо r , а p δ вместо коэффициента дисконтирования δ.

Не забывайте, что вам нужно искать приведенную стоимость только тех убытков (или прибылей), которые будут понесены (или получены) в будущем . Приведенная стоимость 36 долларов, потерянных сегодня, составляет просто 36 долларов. Следовательно, если бы вам потребовалось вычислить приведенную стоимость последовательности убытков по 36 долларов каждый, начиная с текущего дня , вы взяли бы 36 долларов, потерянных сегодня, и прибавили бы к ним приведенную стоимость последовательности убытков, понесенных в будущем. Мы только что вычислили, что она равна 36/ r . Стало быть, приведенная стоимость последовательности убытков в размере 36 долларов, в том числе 36 долларов, потерянных сегодня, составила бы 36 + 36/ r , или 36[( r + 1)/ r ], что эквивалентно 36/(1 — δ). Аналогично, если бы вам понадобилось проанализировать последовательность значений прибыли игрока в случае применения определенной условной стратегии в дилемме заключенных, вам не нужно было бы дисконтировать объем прибыли, полученной за самый первый период; достаточно было бы дисконтировать только те показатели прибыли, которые представляют собой деньги, полученные в будущие периоды.

В играх и стратегических ситуациях, рассмотренных в предыдущих главах, как правило, участвовало всего два или три игрока, поддерживающих взаимодействие. Такие игры распространены в нашей академической, деловой, политической и личной жизни, а значит, их очень важно осмыслить и проанализировать. Тем не менее немало случаев социального, экономического и политического взаимодействия представляют собой стратегические ситуации с одновременным участием множества игроков. Стратегии построения карьеры, инвестиционные планы, маршруты передвижения на работу и обратно в часы пик и даже обучение — все это сопряжено с преимуществами и издержками, зависящими от действий многих людей. Если вы были в одной из этих ситуаций, то, скорее всего, ловили себя на мысли, что что-то здесь не так: например, слишком много студентов, инвесторов и пассажиров толпились именно там, куда нужно было и вам. Или наоборот: желающих поучаствовать в каком-либо благотворительном проекте оказывалось слишком мало, хотя вы и прилагали максимум усилий, чтобы их привлечь. Иными словами, игры со многими участниками, которые ведутся в обществе, часто приводят к результату, не удовлетворяющему большинство, а то и всех его членов. В данной главе мы рассмотрим такие игры с точки зрения уже разработанной нами теории. Это поможет вам понять, что именно в подобных играх идет не так и как с этим бороться.

В самом общем виде игры с участием множества игроков касаются проблем коллективного действия. Лучший способ достижения целей общества в целом или отдельного коллектива — выполнение их членами определенного действия или действий, хотя эти действия не всегда отвечают интересам отдельных людей. Иными словами, наиболее благоприятный для общества исход не обеспечивается автоматически в виде равновесия Нэша. Поэтому мы должны определить, как игра может быть изменена, чтобы она приводила к оптимальному исходу или как минимум улучшала неудовлетворительный исход в случае равновесия Нэша. Но для этого сперва следует понять природу таких игр. Их три типа, и вы с ними уже знакомы: дилемма заключенных, игра в труса и игра в доверие. Несмотря на то что в этой главе основное внимание уделяется играм с одновременным участием множества игроков, мы начнем с уже хорошо знакомых вам игр между двумя участниками.

Представьте, что вы фермер и для вас и соседнего фермера несомненную пользу принесет строительство системы орошения и противопаводковой защиты. Вы можете объединить усилия по реализации этого проекта с соседом или сделать все самостоятельно. Однако после завершения строительства другой фермер автоматически извлечет из него выгоду. Другими словами, каждый из вас заинтересован переложить всю работу на другого. В этом и состоит суть вашего стратегического взаимодействия и проблема коллективного действия.

В главе 4мы уже встречались с подобной игрой, когда каждая из трех соседок принимала решение об инвестициях в уличный сад, которым бы наслаждались все трое. Эта игра стала дилеммой заключенных, и все три ее участницы попытались уклониться от решения вносить вклад; в данной главе анализируется более общий диапазон возможных вариантов структуры выигрышей. Кроме того, в игре «уличный сад» мы оценивали ее исходы по шкале от 1 до 6; в процессе описания общих игр мы рассмотрим и более общие формы преимуществ и издержек в случае каждого игрока.