Авинаш Диксит - Стратегические игры

Точно так же, когда игрок Б делает предложение, он должен выделить игроку А эквивалент x в следующем периоде, а именно ax . Значит, y = 1 — ax . Теперь решить эти уравнения легче. Мы имеем x = 1 — b (1 — ax ), или (1 — ab ) x = 1 — b . Если выразить это уравнение через r и s , оно будет выглядеть так:

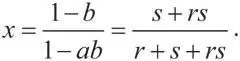
Аналогичным образом y = 1 — a (1 — by ), или (1 — ab ) y = 1 — a . Тогда уравнение примет такой вид:

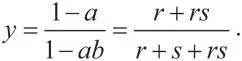
Хотя это быстрое решение может показаться ловким трюком, оно получено в соответствии с теми же действиями, что и используемые ранее; кроме того, немного ниже мы приведем другую аргументацию, дающую точно такой же ответ. Но сначала проанализируем некоторые свойства этого ответа.

Прежде всего обратите внимание, что, как и в примере с разными уровнями терпения, сумма величин x и y больше 1:

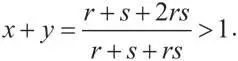
Помните, что x — это то, что получает игрок А, когда он вправе сделать первое предложение, а y — то, что в аналогичном случае получает игрок Б. Когда игрок А делает предложение первым, игрок Б получает (1 — x ), что меньше y ; это подтверждает преимущество игрока А в случае, если он делает первое предложение. Точно так же, когда игрок Б делает предложение первым, он получает y , а игрок А (1 — y ), что меньше x .

Однако r и s — как правило, небольшие числа. Когда предложения могут быть сделаны с короткими промежутками, скажем, через неделю, или один день, или один час, процент, который может быть начислен на ваши деньги за период между ними, или вероятность того, что игра закончится именно на протяжении следующего промежутка, достаточно мала. Например, если r равно 1 % (0,01), а s — 2 % (0,02), то формулы дают x = 0,668 и y = 0,337, а значит, преимущество от права сделать первое предложение составляет всего 0,005. (Игрок А получает 0,668, когда он сам делает первое предложение, но 1–0,337 = 0,663, когда его делает игрок Б; разница — 0,005.) Строго говоря, когда r и s — небольшие числа по сравнению с 1, то их произведение rs на самом деле очень мало; следовательно, мы можем исключить rs из формулы приближенного решения задачи разделения, не зависящей от того, какой игрок делает первое предложение:

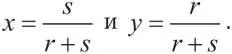
Теперь x + y примерно равно 1.

Важно то, что в приближенном решении x и y — это доли излишка, которые достаются двум игрокам, а y / x = r / s ; другими словами, доли игроков обратно пропорциональны их степени нетерпения, выраженной в виде r и s . Если игрок Б в два раза нетерпеливее игрока А, то игрок А получит в два раза больше, чем игрок Б; значит, их доли составляют 1/3 и 2/3, или 0,333 и 0,667 соответственно. Таким образом, мы видим, что терпение — важное преимущество в переговорах. Наш формальный анализ подтверждает интуитивный вывод о том, что, если вы очень нетерпеливы, другой игрок может предложить вам быструю, но невыгодную сделку, зная, что вы на нее согласитесь.

Эффект нетерпения вредит США, нашим органам власти и дипломатам на многих переговорах с другими странами. Американский политический процесс придает большое значение скорости. Средства массовой информации, заинтересованные группы и конкурирующие политики требуют немедленных результатов и охотно критикуют администрацию или дипломатов за любое промедление. При таком давлении переговорщики всегда испытывают искушение вернуться хотя бы с каким-то решением. Но зачастую эти результаты оставляют желать лучшего в долгосрочной перспективе; уступки других стран содержат различные уловки, а их обещания далеко не достоверны. Правительство США преподносит такие сделки как большую победу, но через несколько лет они, как правило, расторгаются. Финансовый кризис 2008 года — еще один весьма драматичный пример. Когда произошел крах рынка недвижимости, ряд крупных финансовых учреждений, активы которых были обеспечены ипотечными кредитами, очутились на грани банкротства. Это привело к сокращению размера кредитования, что, в свою очередь, поставило экономику США под угрозу глубокого спада. Кризис разразился в сентябре, в разгар президентской кампании. Министерство финансов, Федеральная резервная система и политические лидеры в Конгрессе стремились действовать быстро. Это нетерпение привело к предложению многим финансовым учреждениям гораздо более щедрых условий спасения, тогда как более медленный процесс обеспечил бы налогоплательщикам менее болезненный результат и открыл бы перед ними гораздо более приемлемые перспективы участия в будущих прибылях на спасенные активы.

Когда люди, потерпевшие убытки, ведут со страховой компанией переговоры о страховом покрытии, их позиция намного слабее. Часто компании предлагают тем, кто понес серьезный ущерб, заниженную сумму страхового возмещения, зная, что им необходимо немедленно начать все сначала, а значит, у них высокая степень нетерпения.

На концептуальном уровне формула y / x = r / s связывает подход к переговорам, основанный на некооперативной игре, с кооперативным подходом решения Нэша, о котором говорилось в разделе 1. Выведенная в этом разделе формула для определения долей имеющегося излишка при нулевых значениях BATNA принимает вид y / x = k / h . При кооперативном подходе соотношение между долями двух игроков было таким же, как и соотношение между силой их переговорных позиций, однако предполагалось, что показатели этой силы каким-то образом получены извне. Теперь мы можем объяснить силу переговорных позиций с точки зрения базовых характеристик игроков: значения h и k обратно пропорциональны уровням нетерпения игроков r и s . Иными словами, кооперативному решению Нэша можно дать альтернативную и, возможно, более приемлемую интерпретацию как равновесию обратных рассуждений в некооперативной игре с взаимными предложениями, если мы представим абстрактные показатели силы переговорных позиций в кооперативном решении в виде присущих игрокам характеристик, таких как нетерпение.

И наконец, обратите внимание, что в данном случае соглашение снова может быть достигнуто немедленно, так как самое первое предложение принимается. Как всегда, полный анализ методом обратных рассуждений носит дисциплинирующий характер, поскольку игрок, делающий предложение первым, осознает достоверность того, что другой игрок отклонит менее приемлемый вариант.