Авинаш Диксит - Стратегические игры

Y = A + BX–CX 2 =

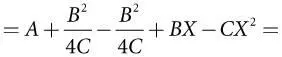
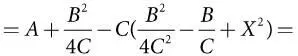
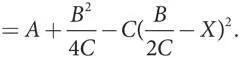
В окончательном варианте формулы X присутствует только в последнем члене, где содержащий это значение квадрат вычитается (помните, что C > 0). Все выражение максимизируется в случае, если его вычитаемый член становится минимальным, что и происходит, если X = B / 2 C . Что и требовалось доказать!

Такой метод дополнения до полного квадрата работает для квадратичных функций, поэтому применим к большинству примеров, рассматриваемых в книге. Однако мы должны признать, что в нем присутствует некий элемент магии. Метод с использованием дифференциального исчисления носит более общий методологический характер, так что изучение основ дифференциального исчисления окупится сторицей.

В главе 3мы рассматривали игры исключительно с последовательными ходами, а глава 4и глава 5посвящены играм только с одновременными ходами. Мы сформулировали концепции и методы анализа, применимые к чистым типам игр, такие как дерево игры и равновесие обратных рассуждений для игр с последовательными ходами, и таблицы выигрышей и равновесие Нэша в играх с одновременными ходами. Однако в реальной жизни многие стратегические ситуации содержат элементы взаимодействия обоих типов игр. Кроме того, хотя мы использовали дерево игры (экстенсивную форму) в качестве единственного метода иллюстрации игр с последовательными ходами и таблицу игры (стратегическую форму) как единственный метод иллюстрации игр с одновременными ходами, каждая из этих форм представления применима к играм любого типа.

В данной главе мы проанализируем многие из этих возможностей. Сначала покажем, как игры, сочетающие последовательные и одновременные ходы, решаются с помощью комбинации деревьев игр и таблицы выигрышей, а также подходящего объединения анализа равновесия обратных рассуждений и равновесия Нэша, затем рассмотрим последствия изменения характера взаимодействия в конкретной игре. В частности, проанализируем результат изменения правил игры в целях преобразования игры с последовательными ходами в игру с одновременными ходами и наоборот и изменения порядка ходов в игре с последовательными ходами. Эта тема позволяет сравнить равновесия, найденные посредством концепции обратных рассуждений в игре с последовательными ходами, с равновесиями, найденными с помощью концепции равновесия Нэша в одновременной версии той же игры. На основании такого сравнения мы расширим концепцию равновесий Нэша на игры с последовательными ходами. Оказывается, равновесие обратных рассуждений — частный случай равновесия Нэша, обычно называемый уточнением.

Как уже неоднократно отмечалось ранее, большинство реальных игр, с которыми вы столкнетесь, будут состоять из множества более мелких компонентов, причем каждый может подразумевать игру либо с одновременными, либо с последовательными ходами, поэтому игра в целом потребует от вас знания обоих типов. Самый очевидный пример стратегического взаимодействия, содержащего как последовательную, так и одновременную составляющую, — это игры между двумя (или более) игроками, продолжающиеся на протяжении длительного периода. За год совместного проживания в комнате вы можете сыграть с соседом в ряд разных игр с одновременными ходами: ваши действия в любой из них зависят от истории вашего общения до нынешнего момента и ваших ожиданий в отношении дальнейших коммуникаций. Кроме того, любые спортивные соревнования, взаимодействие между конкурирующими компаниями в отрасли и политические отношения — все это последовательно связанные серии игр с одновременными ходами. Анализ таких игр подразумевает использование набора инструментов, представленных в главе 3(дерево игры и равновесие обратных рассуждений), главе 4и главе 5(таблица выигрышей и равновесие Нэша) [85]. Единственное различие состоит в том, что фактический анализ усложняется по мере увеличения количества ходов и взаимодействий.

Наш основной иллюстративный пример таких ситуаций касается двух вымышленных крупных телекоммуникационных компаний CrossTalk и GlobalDialog. Каждая из них решает, стоит ли инвестировать 10 миллиардов долларов в покупку волоконно-оптической сети; решение обеими принимается одновременно. Если ни одна не выберет инвестиции, это конец игры. Если одна сделает инвестиции, а другая нет, то компания-инвестор должна установить цены на телекоммуникационные услуги. Она может назначить либо высокую цену, позволяющую привлечь 60 миллионов клиентов, каждый из которых принесет компании операционную прибыль в размере 400 долларов, либо низкую цену, позволяющую привлечь 80 миллионов клиентов, каждый из которых обеспечит компании операционную прибыль в размере 200 долларов. Если обе компании купят волоконно-оптические сети и выйдут на рынок, то ценообразование станет второй игрой с одновременными ходами. Каждая компания может установить либо высокую, либо низкую цену. Если обе предпочтут высокую цену, они разделят рынок поровну и каждая получит 30 миллионов клиентов и операционную прибыль 400 долларов на одного клиента. Если обе выберут низкую цену, они тоже разделят рынок поровну и каждая получит 40 миллионов клиентов и операционную прибыль 200 долларов на одного клиента. Если одна компания установит высокую цену, а другая низкую, то компания с низкой ценой получит все 80 миллионов клиентов, а компания с высокой ценой не получит ничего.

Взаимодействие между CrossTalk и GlobalDialog представляет собой двухэтапную игру. Из четырех возможных комбинаций вариантов выбора в случае игры с одновременными ходами на первом (инвестиционном) этапе одна комбинация завершает игру, две приводят к принятию решения только одним игроком на втором этапе (ценообразования), а четвертая сводится к игре с одновременными ходами (игре в ценообразование) на втором этапе. Игра в графическом виде представлена на рис. 6.1.

Рис. 6.1.Двухэтапная игра, состоящая из последовательных и одновременных ходов

В целом рис. 6.1 иллюстрирует дерево игры, но более сложное, чем в главе 3. Его можно представить как своего рода «дом на дереве» с несколькими уровнями, показанными в разных частях одного двумерного рисунка, как будто вы смотрите на него с вертолета, зависшего непосредственно над ним.