Авинаш Диксит - Стратегические игры

Метод дифференциального исчисления проверяет значение X на оптимальность посредством анализа того, что произойдет со значением функции в случае других значений по любую сторону от X. Если на самом деле X не максимизирует Y = F ( X ), то результатом увеличения или уменьшения X должно быть уменьшение значения Y . Исчисление предоставляет нам возможность быстро выполнить такую проверку.

Рисунок 5П.1 иллюстрирует основную идею. На нем представлен график функции Y = F ( X ), для которого мы использовали функцию, подходящую для наших примеров практического применения теории игр, хотя сама идея носит абсолютно универсальный характер. Начнем с любой точки P с координатами ( X, Y ) на этом графике. Рассмотрим несколько отличающееся значение X , скажем ( X + h ). Пусть k — это итоговое изменение Y = F ( X ), то есть точка Q с координатами ( X + h, Y + k ) также находится на графике. Наклон хорды, соединяющей точки P и Q , — коэффициент k / h . Если значение этого коэффициента положительное, то h и k имеют одинаковый знак: при увеличении X увеличивается и Y . Если значение коэффициента отрицательное, то h и k имеют противоположные знаки, и в случае увеличения X значение Y уменьшается.

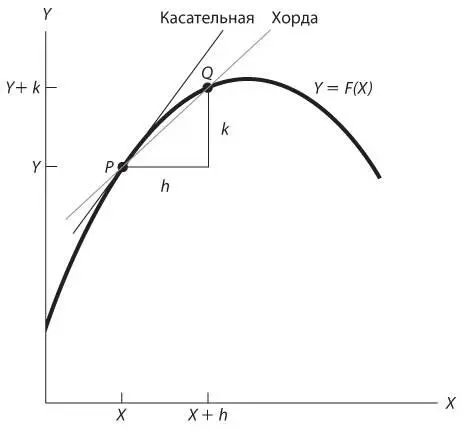
Рис. 5П.1.Иллюстрация к производной функции

Если теперь мы проанализируем все меньшие изменения h значения X и все меньшие изменения k значения Y , хорда PQ будет приближаться к касательной к данному графику в точке P . Наклон этой касательной — и есть предельное значение k/h , называемое производной функцией Y = F ( X ) в точке X . Символически эта производная записывается как F ´( X ) или dY / dX .

Для нашей квадратичной функции имеем

Y = A + BX + CX 2и Y + k = A + B ( X + h ) — C ( X + h ) 2.

Мы можем найти формулу для k следующим образом:

k = [ A + B ( X + h ) — C ( X + h ) 2] — ( A + BX–CX 2) =

Bh — C [( X + h ) 2 — X 2] =

Bh — C ( X 2 + 2 Xh + h 2 — X 2) =

( B — 2 CX ) h — Ch 2.

Тогда k / h = ( B — 2 CX ) — Ch . В пределе, когда значение h стремится к нулю, k/h = ( B — 2 CX ). Последнее выражение и есть производная нашей функции.

Теперь используем эту производную для проверки на оптимальность. На рис. 5П.2 проиллюстрирована эта идея. Точка M дает самое высокое значение Y = F ( X ). Функция возрастает по мере приближения к точке M слева (точка L ) и убывает после удаления от точки M направо (точка R ). Следовательно, производная F ´( X ) должна быть положительной при значениях X меньше M и отрицательной при значениях X больше M. По условию непрерывности производная в точке M должна равняться нулю. На обычном языке это означает, что график функции должен быть плоским в точке максимума, точнее, касательная в этой точке должна быть горизонтальной.

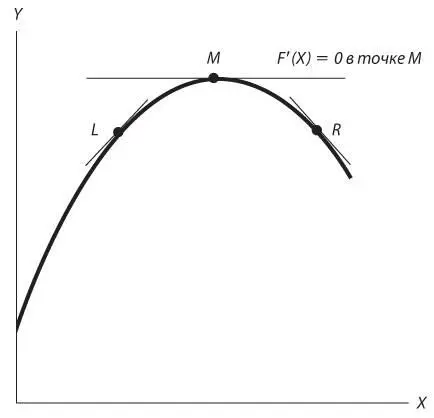
Рис. 5П.2.Оптимум функции

В нашем примере с квадратичной функцией производная равна F ´( X ) = B — 2 CX . Проверка оптимальности подразумевает, что функция имеет оптимум в точке, значение производной в которой равно 0, то есть в точке X = B /2 C . Это и есть та формула, которая приведена в данной главе.

Необходимо выполнить еще одну дополнительную проверку. Если перевернуть график функции, то точка M станет минимальным значением перевернутой функции и в этой самой нижней точке график также будет плоским. Таким образом, для общей функции F ( X ) установление значения F ´( X ) равным 0 позволяет получить значение X , которое обеспечивает как минимум, так и максимум. Как же провести различие между этими двумя возможностями?

В точке максимума функция возрастает слева и убывает справа. Следовательно, производная будет положительной при значениях X меньше предполагаемого максимума и отрицательной при значениях X больше предполагаемого максимума. Иными словами, производная, которая рассматривается как функция от X , убывает в этой точке. Убывающая функция имеет отрицательную производную. Стало быть, производная производной, которая называется второй производной исходной функции и записывается как F ´( X ) или d 2Y / dX 2, должна иметь отрицательное значение в точке максимума. Согласно той же логике вторая производная должна иметь положительное значение в точке минимума — именно это и отличает два случая.

Что касается производной F ´( X ) = B — 2 CX в нашем примере с квадратичной функцией, то применение той же процедуры с h, k по отношению к F ´( X ), что и в случае F ( X ), показывает, что F ˝( X ) = — 2 C . Значение этой производной будет отрицательным при положительном значении C ; именно из такого предположения мы исходили, формулируя задачу в данной главе. Проверка F ´( X ) = 0 называется условием максимизации первого порядка функции F ( X ), а F ˝( X ) < 0 — условием второго порядка.

Для того чтобы закрепить эту идею, применим ее в конкретном примере с наилучшим ответом Xavier’s, который мы рассматривали в данной главе. У нас была такая формула:

П x = — 8(44 + P y ) + (16 + 44 + P y ) P x — 2( P x ) 2.

Это квадратичная функция от P x (при неизменном значении цены другого ресторана P y ). Наш метод позволяет получить ее производную:

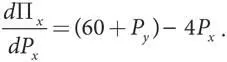
Условие первого порядка для P x для максимизации П x состоит в том, что эта производная должна быть равной нулю. Установив такое значение производной и определив ее значение относительно P x , получим то же уравнение, что и в разделе 1.П. (Условие второго порядка: d 2 П x / dP x 2< 0, и оно удовлетворено, поскольку вторая производная равна −4.)

Мы надеемся, что метод с применением дифференциального исчисления покажется вам достаточно простым и вы сможете использовать его в нескольких местах книги, например в главе 11, посвященной коллективному действию. Однако если вы находите его слишком сложным, предлагаем альтернативный метод без исчисления, который работает в случае квадратичных функций. Перегруппируем члены уравнения, описывающего эту функцию, таким образом: