Авинаш Диксит - Стратегические игры

На рис. 6.12мы начинаем с Талии и исключаем все ее (слабо) доминируемые стратегии. В результате остается только указанная в одиннадцатой строке таблицы, НВВН, которую мы уже вычислили как равновесную, полученную методом обратных рассуждений. Далее мы можем перейти к исключению стратегий Нины, для чего понадобится сравнить исходы, полученные в ходе выбора стратегий, на обеих страницах таблицы. Например, для того чтобы сравнить стратегии Нины ВВ и ВН, необходимо посмотреть на выигрыши, связанные с ВВ на обеих страницах таблицы, и сравнить их с найденными аналогичным способом выигрышами от стратегии ВН. В случае Нины процесс исключения стратегий оставляет ей только стратегию НВ, она и есть равновесная, полученная методом обратных рассуждений выше. И наконец, Эмили нужно всего лишь сравнить две оставшиеся ячейки, связанные с ее выбором «не вносить вклад» и «внести вклад». Эмили получит самый высокий выигрыш, сыграв вариант «не вносить вклад», что она и делает. Как и раньше, мы нашли равновесную стратегию методом обратных рассуждений.

Таким образом, единственный исход в виде совершенного равновесия подыгры соответствует той ячейке таблицы игры на рис. 6.12, которая связана со стратегиями равновесия обратных рассуждений каждого игрока. Обратите внимание, что процесс итеративного исключения стратегий, приводящий нас к совершенному равновесию подыгры, выполняется посредством анализа действий игроков в обратном порядке по сравнению с фактическим ходом игры. Этот порядок соответствует тому, в котором действия игроков анализируются в ходе применения метода обратных рассуждений, что позволяет нам исключать именно те стратегии каждого игрока, которые не согласуются с равновесием обратных рассуждений. При этом мы исключаем из рассмотрения все равновесия Нэша, не являющиеся совершенными равновесиями подыгры.

Многие игры включают в себя множество различных элементов, одни подразумевают одновременное выполнение ходов, тогда как другие сводятся к их последовательному выполнению. Для иллюстрации двухэтапных (и многоэтапных) игр можно использовать своего рода «дом на дереве»: такая схема позволяет идентифицировать различные этапы игры и связи между ними. Полноценные игры, возникающие на более поздних этапах игры, называются подыграми полной игры.

Изменение правил игры в целях изменения времени выполнения ходов может повлиять (или нет) на равновесный исход игры. Игры с одновременными ходами, преобразованные таким образом, чтобы ходы выполнялись последовательно, могут иметь такой же исход (при наличии у обоих игроков доминирующих стратегий), преимущество первого или второго хода, и обеспечивать более благоприятный исход для обоих игроков. Как правило, в последовательной версии игры с одновременными ходами есть единственное равновесие обратных рассуждений, даже если в ее одновременной версии равновесий нет вообще или, наоборот, их множество. Точно так же в игре с последовательными ходами, имеющей единственное равновесие обратных рассуждений, может быть несколько равновесий Нэша, когда правила игры меняются таким образом, чтобы превратить ее в игру с одновременными ходами.

Игры с одновременными ходами можно представить в виде дерева игры, собрав узлы принятия решений в информационные множества , когда игроки принимают решения, не зная о том, в каком именно узле они окажутся. Точно так же игры с последовательными ходами можно проиллюстрировать с помощью таблицы игры, но при этом необходимо точно определить всю совокупность стратегий, имеющихся в распоряжении каждого игрока. В процессе решения игры с последовательными ходами, представленной в стратегической форме, можно найти множество равновесий Нэша. Их количество можно сократить, воспользовавшись критерием достоверности для исключения некоторых стратегий как потенциально равновесных. Данный процесс позволяет отыскать совершенное равновесие подыгры в игре с последовательными ходами. Все эти процедуры поиска решения применимы и к играм с участием большего количества игроков.

Достоверность

Информационное множество

Неравновесные подыгры

Неравновесные пути игры

Подыгра

Продолжение стратегии

Совершенное равновесие подыгры

S1.Рассмотрите игру с одновременными ходами с участием двух игроков, в которой нет равновесия Нэша в чистых стратегиях, представленную на рис. 4.13 в главе 4. Если бы эта игра была преобразована в игру с последовательными ходами, вы бы ожидали появления в ней преимущества первого и второго хода или ни одного из них? Объясните логику своих рассуждений.

S2.Рассмотрите игру, представленную в виде дерева игры ниже. Игрок, делающий ход первым (Игрок 1), может выбрать ход либо «вверх», либо «вниз», после чего Игрок 2 может выбрать «налево» или «направо». Выигрыши в случае возможных исходов указаны в концевых узлах дерева. Изобразите эту игру в стратегической форме (в виде таблицы). Найдите все равновесия Нэша в чистых стратегиях. Если их несколько, укажите, какое из них представляет собой совершенное равновесие подыгры. Для равновесий, не являющихся таковыми, определите причину (источник отсутствия достоверности).

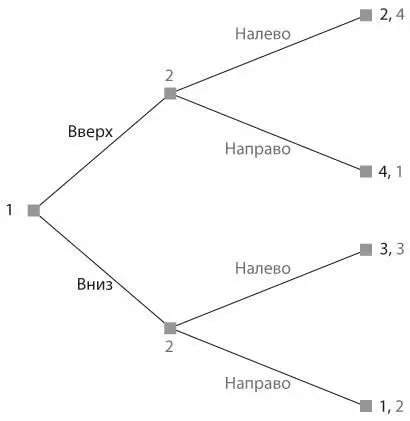
S3.Рассмотрите игру между Airbus и Boeing, описанную в упражнении S4 в главе 3. Представьте ее в стратегической форме и определите все равновесия Нэша. Какое из них представляет собой совершенное равновесие подыгры? Для равновесий, не являющихся таковыми, определите источник отсутствия достоверности.

S4.Вернитесь к дереву игры с двумя участниками, приведенному в пункте а упражнения S2 в главе 3.

a) Изобразите эту игру в стратегической форме, где Страшиле соответствуют строки, а Железному Дровосеку — столбцы.

b) Найдите равновесие Нэша.

S5.Вернитесь к дереву игры с двумя участниками, приведенному в пункте b упражнения S2в главе 3.

a) Представьте эту игру в стратегической форме. (Подсказка: используйте решение упражнения S2в главе 3.) Найдите все равновесия Нэша (их будет много).

b) Для равновесий, найденных в пункте а, которые не являются совершенными равновесиями подыгры, определите проблемы с достоверностью.

S6.Вернитесь к дереву игры с тремя участниками, приведенному в пункте с упражнения S2 в главе 3.

a) Составьте таблицу этой игры. Сделайте Страшилу игроком, которому соответствуют строки, Железному Дровосеку — столбцы, а Льву — страницы. (Подсказка: используйте решение упражнения S2в главе 3.) Найдите все равновесия Нэша (их будет много).