Иэн Стюарт - Математические головоломки профессора Стюарта

– Еще какое, Ватсап. Это позволяет пролить совершенно новый свет… опять же, извините за каламбур… на одно из самых невероятных наших нераскрытых дел.

– Замечательное дело перевернутого чайника! – воскликнул я.

– Вот именно, Ватсап! Итак, если в ваших записях сохранилась информация о том, справа или слева от мумифицированного попугая лежала та спичка…

Анализ Сомса основан на:

Maurice Brearley, 'Oar arrangements in rowing eights', in Optimal Strategies in Sports (ed. S. P. Ladany and R. E. Machol), North-Holland 1977.

John Barrow, One Hundred Essential Things You Didn't Know You Didn't Know, W. W. Norton, New York 2009.

Как и предупреждал Сомс, это лишь первоначальный упрощенный подход к весьма сложной проблеме.

Кстати говоря, Университетская гонка 1877 г. закончилась ничьей – единственный случай в истории этих состязаний.

Джон Мейсон и Теодорус Деккер нашли более простые методы доказательства невозможности, чем те, которыми пользовался Сверчковский. При склеивании двух одинаковых тетраэдров гранями каждый из них становится как бы отражением другого в их общей грани.

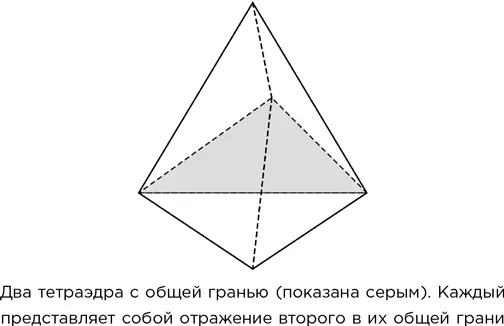
Начнем с одного тетраэдра. У него четыре грани и, соответственно, четыре таких отражения; назовем их r 1, r 2, r 3и r 4. Каждое отражение ставит все на прежнее место, если проделать операцию дважды, так что r 1 r 1= e , где e – это нулевая трансформация («ничего не делать»). То же можно сказать и об остальных отражениях. Таким образом, все комбинации нескольких отражений представляют собой произведения вроде такого:

r 1 r 4 r 3 r 4 r 2 r 1 r 3 r 1,

где последовательность индексов 14342131 может быть любой последовательностью чисел 1, 2, 3, 4, где ни одно число не встречается два раза подряд. К примеру, последовательности 14332131 быть не может. Причина в том, что здесь r 3 r 3 – это одно и то же отражение, проделанное дважды, то есть e , которое не производит никакого действия и потому может быть исключено.

Если такая цепочка замыкается, то очередное отражение, примененное к крайнему тетраэдру в цепочке, дает тетраэдр, который совпадает с первоначальным. Таким образом, мы получаем уравнение вида

r 1 r 4 r 3 r 4 r 2 r 1 r 3 r 1= e

(только более длинное и сложное), где e означает «ничего не делать». Записав формулы для четырех отражений и воспользовавшись подходящими алгебраическими методами, можно доказать, что такое уравнение не выполняется никогда. Подробности см.:

T. J. Dekker, On reflections in Euclidean spaces generating free products, Nieuw Archief voor Wiskunde 7 (1959) 57–60.

M. Elgersma and S. Wagon, Closing a Platonic gap, Mathematical Intelligencer in the press.

J. H. Mason, Can regular tetrahedrons be glued together face to face to form a ring? Mathematical Gazette 56 (1972) 194–197.

H. Steinhaus, Problem 175, Colloquium Mathematicum 4 (1957) 243.

S. Swierczkowski, On a free group of rotations of the Euclidean space, Indagationes Mathematicae 20 (1958) 376–378.

S. Swierczkowski, On chains of regular tetrahedra, Colloquium Mathematicum 7 (1959) 9–10.

– Как вы правильно сказали, вы их не видите, – сказал Сомс. – Вы же знаете мои методы: воспользуйтесь ими.

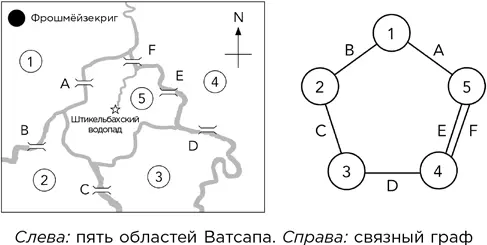
– Очень хорошо, Сомс, – ответил я. – Вы всегда говорили, что нужно отбросить все несущественное. Поэтому я повторю свои рассуждения, а чтобы устранить всякую мыслимую возможность ошибки, представлю задачу в простейшем виде. Я пронумерую области на карте – вот так. Их пять. Затем я нарисую диаграмму – кажется, она называется графом, – на которой схематически покажу эти области и связи между ними.

Он молчал с непроницаемым выражением лица.

– Мы должны попасть из области 1 в область 5, причем мост A должен быть последним. Если начинать из 1, единственным оставшимся вариантом будет пересечь мост B, затем неизбежно последуют C и D. Далее мы должны воспользоваться мостом E или F. Скажем, мы выбрали мост E. Далее мы не можем воспользоваться F, потому что это приведет нас в область 4, из которой далее пути для нас нет. Однако мы не можем воспользоваться и мостом A, потому что это приведет нас в область 1, из которой пути нет. То же произойдет, если мы выберем F вместо E. Я закончил.

– Почему, Ватсап?

– Потому, Сомс, что я исключил невозможное, – он поднял бровь. – Поэтому то, что останется, каким бы невероятным оно ни казалось, – продолжал я, – должно быть…

– Продолжайте.

– Но, Сомс, ничего не остается! Следовательно, задача не имеет решения!

– Неверно. Я уже сказал вам, что решений здесь восемь.

– Тогда вы, вероятно, солгали мне об условиях задачи.

– Нет.

– Тогда я в тупике. Что я упустил?

– Ничего.

– Но…

– Вы кое-что впустили , Ватсап. Вы слишком многое приняли за данность. Вы ошибочно решили, что маршрут не должен выходить за пределы нарисованной мной карты.

– Но вы же сказали, что дальше реки текут до границ Швейцарии и дальше, а нам нельзя пересекать границу.

– Да. Но на карте изображена не вся Швейцария. Откуда течет эта река?

– О-ох! – я хлопнул себя ладонью по лбу.

– Кто? Бог?

– Просто непроизвольное выражение. Я браню себя за собственную глупость, Сомс. Не «Бог», скорее просто «О-ох!».

– Я посоветовал бы вам избегать этого выражения, Ватсап. Оно вам не идет, да и модным никогда не станет.

– Как скажете, Сомс. Моя вспышка была вызвана тем, что я понял: мою вторую попытку можно завершить, если обогнуть исток реки и пройти по мосту A.

– Верно.

– Так что области 1 и 4 на моем рисунке – на самом деле одна и та же область.

– В самом деле. Это, – сказал я через мгновение, – было нечестно. Откуда мне знать, что исток реки находится в границах Швейцарии? Он не показан на вашей карте.

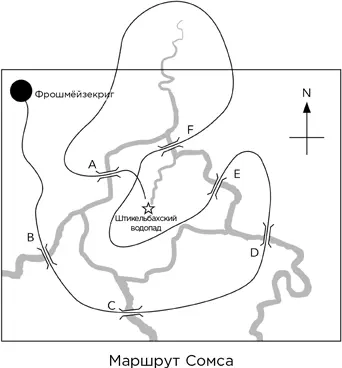
– Но ведь я сказал вам, Ватсап, что существует по крайней мере один маршрут, удовлетворяющий всем условиям. Из этого однозначно следует, что исток реки должен находиться в Швейцарии.

Туше. Я вспомнил также, что он говорил про восемь маршрутов.

– Я вижу второй маршрут, Сомс: достаточно поменять местами мосты E и F. Но остальные шесть, признаюсь, от меня ускользают.

– Ах. Ваше утверждение, что начинать мы должны непременно с моста B, теряет смысл, если области 1 и 4 сливаются. Позвольте мне перерисовать вашу упрощенную схему правильно.