Саймон Сингх - Симпсоны и их математические секреты

Из личного архива Майка Рейсса

Если n – это количество периодов начисления сложного процента (другими словами, сколько раз в год он рассчитывается и прибавляется к основной сумме), то для расчета окончательной суммы ( F ) можно использовать следующую формулу:

F = $(1 + 1⁄n) n

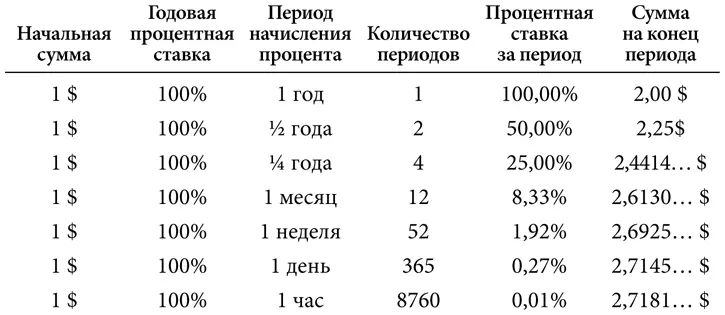
В случае начисления сложного процента один раз в неделю мы получаем почти на 0,70 доллара больше процентного дохода, чем при начислении простого годового процента. Однако дальнейший расчет сложного процента с еще большей периодичностью обеспечивает совсем незначительное увеличение процентного дохода. Здесь и возникает занимательный вопрос, который очень интересует математиков: если бы сложный процент рассчитывался не только каждый час и даже каждую секунду или микросекунду, а каждое мгновение, то какой была бы сумма на конец года?

Вот вам ответ: 2,718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427… доллара. Наверное, вы догадываетесь, что количество десятичных знаков стремится к бесконечности, а значит, это иррациональное число. Именно его мы и называем числом e .

Число 2,718 обозначено символом e , поскольку оно связано с понятием экспоненциального роста , описывающим поразительные темпы роста в случае, если деньги приносят процент из года в год или нечто другое снова и снова увеличивается фиксированными темпами. Например, если бы стоимость вложенной суммы действительно увеличивалась в 2,718… раза год за годом, то через год 1 доллар превратился бы в 2,72 доллара, через два года это было бы уже 7,39 доллара, через три – 20,09 доллара, затем 54,60 доллара, потом 148,41 доллара, 403,43 доллара, 1096,63 доллара, 2980,96 доллара, 8102,08 доллара и наконец 22 026,47 доллара всего за десять лет.

Столь поразительный темп устойчивого экспоненциального роста редко встречается в мире финансовых инвестиций, но есть конкретные примеры в других областях. Самый показательный пример имел место в сфере технологий и известен как закон Мура , который так назван по имени одного из основателей компании Intel Гордона Мура. В 1965 году Мур подметил, что количество транзисторов, размещаемых на интегральной схеме, удваивается примерно каждые два года, и предсказал, что эта тенденция будет продолжаться. Как и следовало ожидать, закон Мура выполнялся десятилетие за десятилетием. За сорок лет, с 1971 по 2011 год, количество транзисторов удваивалось двадцать раз. Другими словами, за четыре десятка лет их число на интегральной схеме увеличилось в 2 20раз, или примерно в один миллион раз. Именно поэтому у нас теперь есть микропроцессоры с огромной производительностью, себестоимость производства которых существенно снизилась по сравнению с 1970-ми годами.

По аналогии с законом Мура иногда говорят, что если бы производство автомобилей росло таким же стремительными темпами, что и производство компьютеров, то автомобиль Ferrari стоил бы сейчас 100 долларов и мог бы проехать миллион километров на одном литре бензина… но и ломался бы каждую неделю.

Тот факт, что число e связано со сложным процентом и экспоненциальным ростом, – очень интересен, но данное число может предложить миру кое-что еще. Подобно числу π, число e всплывает в самых разных ситуациях.

Например, число e лежит в основе так называемой задачи о беспорядках , более известной как задача о шляпах . Представьте, что вы работаете в гардеробе ресторана – принимаете у клиентов шляпы и складываете их в коробки для шляп. К сожалению, вы не отмечаете, кому какая шляпа принадлежит. Когда посетители ресторана, поужинав, приходят за своими шляпами, вы отдаете им коробки со шляпами в случайном порядке и прощаетесь, прежде чем они их открывают. Какова вероятность того, что ни в одной из коробок не находится шляпа, принадлежащая человеку, которому вы только что вручили коробку? Ответ зависит от количества клиентов ( n ), а вероятность отсутствия совпадений P( n ) можно вычислить по следующей формуле [42]:

Таким образом, в случае одного посетителя вероятность отсутствия совпадений составляет 0, поскольку одна шляпа неизбежно попадет к своему владельцу:

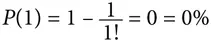
В случае двух посетителей вероятность отсутствия совпадений равна 0,5:

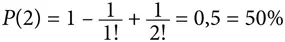
В случае трех посетителей вероятность отсутствия совпадений составляет 0,333:

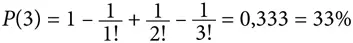
Для четырех клиентов вероятность равна примерно 0,375, а для десяти – около 0,369. Если количество клиентов стремится к бесконечности, значение вероятности становится 0,367879…, что составляет 1/2,718…, или 1/ e .

Вы можете сами проверить эту закономерность, взяв две колоды карт и перетасовав их по отдельности, чтобы карты в каждой колоде располагались произвольным образом. Одна колода символизирует случайный порядок, в котором шляпы укладывались в коробки, а другая – случайный порядок, в котором клиенты возвращались за своими шляпами. Положите обе колоды рядом друг с другом и переворачивайте по одной верхней карте в каждой колоде. Если обе карты имеют одинаковую масть и значение, это засчитывается как совпадение. Вероятность отсутствия совпадений после просмотра всех карт обеих колод близка к 1/ e , что составляет примерно 0,37, или 37 процентов. Другими словами, если вы будете повторять весь процесс сотню раз, то вас ждет не слишком активная светская жизнь и примерно тридцать семь колод карт с отсутствием совпадений. Хотя задача о шляпах может показаться тривиальной, она представляет собой фундаментальный вопрос такой области математики, как комбинаторика .

Число e также появляется в процессе изучения кривой особого типа, известной под названием катенарная кривая [43], поскольку она имеет форму цепи, провисшей между двумя точками. Этот термин, придуманный Томасом Джефферсоном, происходит от латинского слова catena , что означает «цепь». Форма катенарной кривой описывается следующим уравнением, в котором присутствует два числа e :

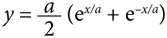
Шелковая нить в паутине образует ряд катенарных кривых между лучами паутины, что подтолкнуло французского энтомолога Жана Анри Фабра написать в книге The Life of the Spider («Жизнь пауков») следующее: «Здесь снова появляется похожее на абракадабру число e , начертанное на нитях паутины. Давайте посмотрим туманным утром, какая сетчатая структура была создана за ночь. Липкие нити, имеющие гидрометрические свойства, провисают под тяжестью крохотных капель воды и образуют множество катенарных кривых – нитей прозрачных жемчужин, изящных бус, расположенных в изысканном порядке и повторяющих форму кривой качания. Когда солнечные лучи пронизывают пелену тумана, все это начинает светиться разноцветными огнями и напоминает сверкающие нити бриллиантов. Это и есть число e во всем своем великолепии».