Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Гранд-мофф Таркин. Бедняга-геометр потратил месяцы на мозговые штурмы, заполняя блокноты эскизами и конструкторскими идеями… Лорд Вейдер возненавидел их все.

Дарт Вейдер . Шестиугольная призма? Мы что, империя медоносных пчел?

Имперский геометр . Даже в самых глубоких ущельях неверия в собственные силы я был благодарен лорду Вейдеру за обратную связь. Он требовательный управленец, как и многие визионеры. Но я знаю, что все это было в рамках конструктивной критики.

Дарт Вейдер . Кретин.

Имперский геометр. В конце концов мы выявили единственный целевой показатель: симметрию.

Большинство людей небрежно пользуются этим термином, но в математике слово «симметрия» имеет точное определение: то, что можно сделать с фигурой, чтобы она выглядела так же, как раньше.

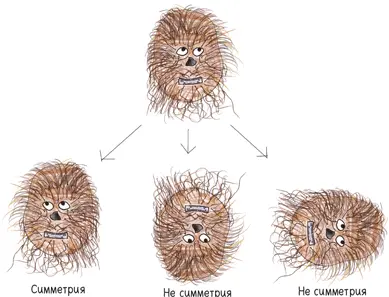
Например, морда вуки имеет одну-единственную симметрию: ее можно отразить в вертикальном зеркале {36} 36 Не обращайте внимания на направление взгляда вуки, только на форму морды. — Прим. науч. ред. . Вот и все. Если вы проделаете что-нибудь еще (скажем, повернете ее на 90° или отразите в горизонтальном зеркале), вы измените его морду до неузнаваемости, после чего вуки может попытаться изменить до неузнаваемости вашу физиономию.

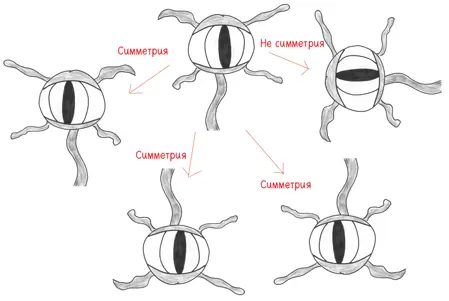
Напротив, морда дианоги [67] Благодарю Грегора Назариана, который смягчил мое сердце, как музыкальная тема Джона Уильямса, и помог существенно улучшить эту главу. (Я упоминаю его здесь, потому что он подсказал мне идею с дианогой, а не потому, что его лицо напоминает дианогу.) (болотной обитательницы с щупальцами, которая иногда заводится в мусорных контейнерах) обладает тремя симметриями: два отражения и поворот на 180° {37} 37 А тут не обращайте внимание на щупальца, иначе все будет как у вуки. — Прим. науч. ред. .

Гранд-мофф Таркин. Зачем зацикливаться на симметрии? Ну, симметрия — суть красоты.

Посмотрим, скажем, на человеческие лица. Ни одно не симметрично идеально. Одно ухо чуть повыше; один глаз чуть побольше; нос слегка кривоват. Но чем симметричнее лицо, тем красивее оно нам кажется. Странный психологический факт: математика — мерило красоты.

Мы стремились, чтобы «Звезда смерти» сражала наповал, как лицо супермодели.

Имперский геометр . Однажды лорд Вейдер смел мои чертежи со стола и зарычал: «БОЛЬШЕ СИММЕТРИИ!» Мы рассматривали икосаэдр, у которого 120 симметрий. Как я мог добиться большего? Но потом я все-таки нашел решение, и я больше всего горжусь этим моментом моей карьеры — нет, черт возьми, всей моей ЖИЗНИ. Я нашел решение: максимально симметричное геометрическое тело.

Дарт Вейдер. Почему ему сразу не пришло в голову начать с шара? Черепашья скорость немощных мозгов отнимает слишком много времени.

Гранд-мофф Таркин. Головная боль никуда не делась. Нам необходимо было установить набор лазеров, уничтожающих планеты, в северном полушарии «Звезды смерти» и тем самым нарушить симметрию. Нам это сильно попортило кровь.

Имперский геометр . Я по-прежнему убежден: монтировать этот лазер было ошибкой. Я имею в виду, что эффективнее для устрашения — небольшое лазерное шоу или БЕСКОНЕЧНОЕ число симметрий?

Гранд-мофф Таркин. Мы сразу же столкнулись с трудностью. Можно сказать, со встречным ветром.

Все бывали внутри «Звездных разрушителей» и помнят эти сверкающие угловатые конструкции. Они были галактическими ножами для стейков, готовыми вспороть любую звезду, как воздушный шарик с гелием. Когда я осознал, что дизайн должен быть не только эстетичным, но и функциональным, это доставило неприятности нашей станции.

Имперский физик . Представьте, что вы летите на аэроплане. Неважно, насколько вы хороший пилот, все равно вас ждет ЧРЕЗВЫЧАЙНО много столкновений. Я имею в виду, разумеется, столкновения с молекулами воздуха.

Наилучший сценарий? Молекулы воздуха скользят ПАРАЛЛЕЛЬНО поверхности вашего самолета. Таким образом, они никак не влияют на ваше движение. Они похожи на поток автомобилей на встречной полосе. Наихудший сценарий: молекулы воздуха двигаются ПЕРПЕНДИКУЛЯРНО поверхности самолета, под углом 90°. Тогда все молекулы в полной мере влияют на ваше движение. Вот почему вы не станете строить аэроплан с большой, плоской фронтальной поверхностью: он будет похож на человека-сэндвича с рекламными щитами, пробивающегося сквозь толпу.

Поэтому «Звездный разрушитель» имеет клиновидную форму. Когда он летит сквозь атмосферу, молекулы воздуха в основном скользят вдоль его бортов — почти параллельно поверхности. Напротив, «Звезда смерти» стала нашим аэродинамическим ночным кошмаром. Ее огромная поверхность вынуждена сталкиваться с молекулами воздуха под практически идеально прямым углом.

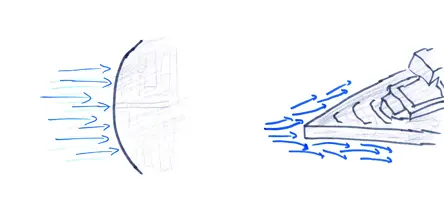
Имперский инженер. Представьте, что ваши друзья запускают бумажные самолетики, но, вместо того чтобы составить им компанию, вы кидаете парту через весь класс. Вы потратите существенно больше энергии, а парта будет лететь не слишком изящно.

Гранд-мофф Таркин. Изначально мы предполагали, что «Звезда смерти» будет непосредственно посещать планеты. Она должна была входить в атмосферу и испепелять континент или пару континентов, пока из динамиков звучит «Имперский марш».

Эта мечта умерла, когда мы выбрали форму шара. Аэродинамика расстроила наши планы, и наша станция вынуждена была оставаться в космическом вакууме. Никакого сопротивления воздуха — но и никакой музыки.

Дарт Вейдер. Мы пошли на жестокую жертву. Но вожди не должны быть малодушны.

Гранд-мофф Таркин. Вскоре на нашем пути возникла очередная сложность: наши физики продолжали настаивать на том, что «Звезда смерти» обречена приобрести форму бугристого астероида.

Имперский физик. Бросьте взгляд на галактику. Где вы видите шары? Они большие и тяжелые. Звезды, планеты, несколько крупных спутников. А теперь взгляните на мелкие объекты с меньшей плотностью: астероиды, кометы, облака пыли. Вы обнаружите множество уродливых картофелин.

Совпадение? Не думаю. Это факт гравитации. Я с самого начала говорил им: «Звезда смерти» слишком мала, чтобы стать шаром.