Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Имперский геометр. Ах, это еще одна причина, по которой шар был идеальной формой! При заданном объеме он обладает наименьшей плотностью поверхности. Если вы строите корпус для огромного устройства, скажем лазерной пушки, сокрушающей планеты, сферическая форма позволит израсходовать минимум материала.

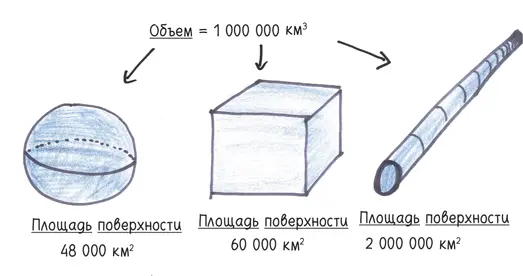
Имперский инженер. Я знаю, геометр скажет, что сферическая форма сэкономит наши деньги, потому что для куба понадобится на 24 % больше стали. Типичный математик: сплошное теоретизирование, никакой практичности.

Есть причина, по которой мы не имеем обыкновения строить космические корабли в форме сферы: кривизна — это мука мученическая! Вы когда-нибудь пробовали расставить мебель в изогнутой комнате? Желаю удачи с размещением дивана.

Впрочем, «Звезда смерти» была слишком велика, чтобы заметить искривление на таком уровне. Никаких проблем для дизайнеров интерьера. Но с точки зрения строительства кривизна обеспечила мне головную боль на много лет. Нам нужны были стальные балки с кривизной 0 градусов, 0 угловых минут и 3 угловых секунды на метр — меньше чем 1 градус на километр.

Это черт знает что! Кривизна была настолько низкой, что ее нельзя было заметить невооруженным глазом, но в то же время настолько высокой, что отдельные элементы нужно было изготовлять на заказ.

Гранд-мофф Таркин. Изогнутые балки… О, не напоминайте. Один субподрядчик поставлял нам прямые балки целый год — и думал, что мы не заметим. Честно говоря, мы и правда не заметили, пока однажды Император не приблизился на шаттле и не сказал: «Что это за смешная выпуклость?» Мы были отброшены на МЕСЯЦЫ назад. Но, во всяком случае, субподрядчику пришлось страдать гораздо больше, чем нам.

Дарт Вейдер. Эти субподрядчики — сплошные идиоты. Можно надуть обычных клиентов, но не Империю зла.

Имперский геометр. Как я уже сказал, шар имеет минимальную площадь поверхности при заданном объеме. Но я признаю, что у этой формы есть свои недостатки.

Гранд-мофф Таркин. Ликвидация мусора стала вечной пыткой.

Имперский мусорщик . Основное решение проблемы мусора в космосе просто: выбросить его за борт. Однако минимальная площадь поверхности означает, что большая часть вашей станции расположена далеко от поверхности. Нам понадобились мусоропроводы длиной в десятки километров. Я начал кампанию по переработке отходов, но экипаж просто выбрасывал все — еду, стальные балки, живых повстанцев, взятых в плен, — в мусорные контейнеры. Я не мог избавиться от чувства, что экология там не была приоритетным направлением.

Имперский инженер. Меня до сих пор преследует проблема отопления. Открытый космос, верно? Там прохладно. Если вы хотите сохранить тепло, шарообразная форма подходит идеально. Минимальная площадь поверхности означает минимальные потери тепла. Однако, по всей видимости, мы поработали СЛИШКОМ хорошо, потому что первичное моделирование показало, что станция имеет тенденцию к перегреву.

Имперский проектировщик . Нам пришлось избавляться от излишков тепла, поэтому я добавил теплоотводные шахты. Ничего особенного. Шириной в несколько метров. Тепло уходит в космос; проблема решена.

Мне и голову не приходило…

Я имею в виду, когда я узнал, что повстанцы уничтожили станцию, добравшись до теплоотводной шахты… [71] Я не уверен, что успешно вплел это повествование в канву событий с учетом нового фильма «Изгой-один». Вне всяких сомнений, вольности, которые я себе позволил, огорчат по-настоящему непреклонных и достойных восхищения блюстителей канона. С другой стороны, я дал этим персонажам доступ к данным переписи в Западной Вирджинии за 2010 год, поэтому, возможно, перераспределение конструкторских заслуг — еще не худшее мое прегрешение. [Вероятно, самая большая вольность — воскрешение гранд-моффа Таркина ради этого интервью. В фильме он погиб вместе со «Звездой смерти». — Прим. пер. ]

Адвокат имперского проектировщика. Пусть запись покажет: следственная группа обнаружила, что «Звезда смерти» была уничтожена дефектным реактором, которого мой клиент НЕ проектировал. Вкладом моего клиента были теплоотводные шахты. Они успешно справлялись со своей задачей — выпускать тепло за пределы станции.

Дарт Вейдер. Кроме того, они успешно впустили протонную торпеду ВНУТРЬ станции.

Гранд-мофф Таркин . От туманного начала до горького конца «Звезда смерти» была плодом компромиссов. Она была дорогостоящей? Да. Неэффективной? Вне всяких сомнений. Уничтожена шайкой подонков-повстанцев? Сложно отрицать.

И все же… Я никогда ничем так не гордился, как этим огромным, достославным шаром.

Издалека он был похож на Луну с кратером от астероида. Затем вы приближались, и геометрическое совершенство ошарашивало вас: бесчисленные симметрии этого кратера, прямые углы каналов на поверхности, темный опоясывающий рубец на экваторе…

Имперский геометр. «Звезда смерти» осуществила жуткий синтез: настолько грандиозная, каким может быть лишь небесное тело, и настолько идеальная, каким оно не может быть никогда. Она была волнующей, неотразимой, ужасающей. В этом сила геометрии.

Дарт Вейдер. Как это часто бывает, наши критики придумали нам лучший слоган. Когда мой старый заклятый друг Оби-Ван сказал: «Это не Луна!», мы поняли, что теперь у нас есть лозунг для рекламы.

Вы хоть раз в жизни играли в орлянку? Готов поспорить, что да, если вы не настолько обнищали, что у вас нет даже мелочи, или не настолько купаетесь в деньгах, чтобы утруждать себя поиском монет. Также я подозреваю, что, несмотря на шансы 50/50, каждый конкретный исход не был помесью орла и решки. Либо орел, либо решка. Все или ничего.

Такова жизнь: она полна случайных точечных событий. Непредвиденных задержек поездов. Волевых побед. Свободных мест на парковке, магическим образом возникающих из ниоткуда. В нашем мире, где бушуют ураганы, может произойти все что угодно, и судьба никогда не высылает оповещений загодя.

Но если бы вы могли подкинуть монетку триллион раз, вы бы оказались в совершенно другом мире: опрятная вселенная, где все ясно в долгосрочной перспективе. 50 % раз выпадает орел, половина новорожденных — мальчики, события с вероятностью одна миллионная происходят единожды из миллиона случаев (или что-то около того). В этом абстрактном царстве с вечно голубыми небесами нет никаких заскоков и случайных совпадений. Они тонут в совокупности всех возможных исходов, как галька, брошенная в море.