Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Теория вероятностей наводит мосты между этими двумя мирами. В нашем — диком и запутанном — ни в чем нельзя быть уверенным. В спокойном же, просчитанном мире, которого нам никогда не достичь, все заранее предрешено. Специалист по теории вероятностей — гражданин двух миров одновременно, он пытается рассматривать каждый сенсационный заголовок и низвержение знаменитостей как одну из карт бесконечной колоды, горсть воды из бездонного кувшина. Мы, смертные, никогда не войдем в пределы вечности, но теория вероятностей дарит нам проблеск надежды.

Ах, лотерейный билет. Cертификат оптимизма, казначейская облигация Министерства надежды. Зачем держаться за потрепанную однодолларовую купюру с загнутыми уголками, если можно обменять ее на непредсказуемую сумму от нуля до $50 млн?

Если для вас это звучит непривлекательно, что же, вы и все человечество будете просто вынуждены поменять свое мнение.

Должен признаться, я потратил на лотерейные билеты меньше денег за всю жизнь (семь долларов), чем на круассаны за текущий месяц (не спрашивайте сколько). Тем не менее ежегодно в лотерею играют около половины взрослых американцев. Это не та половина, о которой вы, вероятно, подумали. Люди с ежегодным доходом $90 000 играют чаще, чем те, кто зарабатывает меньше $36 000 [72] Zac Auter, «About Half of Americans Play State Lotteries», Gallup News, July 22, 2016, http://news.gallup.com/poll/193874/half-americans-play-state-lotteries.aspx . Однако по-прежнему верно, что лотерея — своего рода «регрессивный налог», потому что, если бедный человек тратит ту же сумму денег, что богатый, она составляет больший процент его дохода. . Те, у кого есть степень бакалавра, играют чаще, чем те, у кого ее нет. Больше всего денег на лотерею расходуют жители моего родного штата Массачусетс: пристанище обеспеченных, суперобразованных либералов, которые тратят на лотерейные билеты за год в среднем по $800 на человека [73] DiFiore, «15 States Where People Spend the Most on Lotto Tickets», Credit.com, July 13, 2017, https://www.marketwatch.com/story/the-states-where-people-spend-the-most-on-lotto-tickets-2017-07-24 . Хотя статистика меняется из года в год, Массачусетс остается среди лидеров по этому показателю с 1987 года (между прочим, это год моего рождения). . Играть в лотерею, как и смотреть футбол, судиться с соседями или распевать национальный гимн, — это американский вид досуга, и ему предаются по разным причинам.

Идем, составьте мне компанию в очереди за лотерейным билетом, и мы исследуем многогранную привлекательность инвестиций с шансом на коммерческий успех.

Смотрите-ка! Это Заядлый Игрок, который покупает лотерейные билеты по той же причине, по какой я покупаю круассаны: не ради пропитания, а ради удовольствия.

Возьмем для примера популярную в Массачусетсе лотерею «Приз $10 000 наличными» [74] Информация с сайта MassLottery.com: https://www.masslottery.com/games/instant/1-dollar/$10k-bonus-cash-142-2017.html . . Гениальное название. Поставьте рядом слово «приз» и число 10 000, и вы никогда не прогадаете, о чем бы там ни шла речь дальше [75] Попробуем. «Приз 10 000 тортилий», «Приз 10 000 рукопожатий», «Приз 10 000 обнимашек с щенками». Да, это беспроигрышный зачин. . К тому же иллюстрация на лотерейном билете за один доллар выглядит как фото в ночном рейв-клубе, распечатанное на цветном принтере. На обороте вы найдете следующую сложную таблицу шансов на победу.

Сколько выиграет ваш билет? Ну, пока что мы не в курсе. Может быть, $10 000; может быть, пять долларов; может быть (я имею в виду «скорее всего»), ничего.

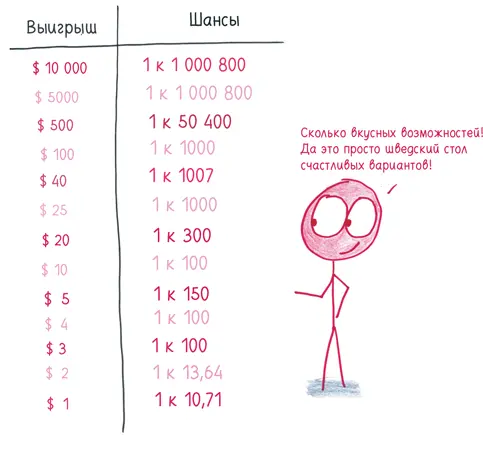
Было бы неплохо оценить выигрыш с помощью одного-единственного числа. Представьте, что мы потратили не один жалкий доллар, а миллион долларов. Таким образом, мы сбежали из толчеи на танцполе нашего мира кратковременности в тихий и мирный мир долговременности, где каждый выигрыш случится с известной заранее вероятностью. Когда мы купим миллион билетов, событие с вероятностью одна миллионная, скорее всего, произойдет один раз {39} 39 Но примерно с такой же вероятностью не произойдет вовсе — автор пока что находится в той же области торжествующей случайности, из которой он хотел сбежать. — Прим. науч. ред. . Событие с вероятностью 1 к 100 000 произойдет примерно десять раз. Событие с вероятностью 1 к 4 произойдет примерно 250 000 раз (или что-то около того).

Возбужденно раскладывая наши билеты по стопкам, мы ждем, что наш выигрыш распределится примерно следующим образом:

Около 20 % наших билетов оказались выигрышными [76] Примерно половина из них просто вернула вам потраченный доллар, поэтому, возможно, стоит сказать не «выигрышные», а «непроигрышные». . Если суммировать все деньги, инвестиции размером в миллион долларов принесли нам около $700 000… и это означает, что $300 000 из нашего кармана перешли прямиком в казну штата Массачусетс.

Иными словами, каждый билет стоимостью один доллар принес нам около 70 центов.

Математики называют это число ожидаемым выигрышем {40} 40 В данном случае речь идет об азартных играх, поэтому используется термин теории выбора. В других случаях «expected value» принято переводить как «математическое ожидание». — Прим. пер. от покупки одного билета. Я понимаю, что это забавный термин, потому что вы не ждете, что каждый билет принесет 70 центов, — точно так же вы не ждете, что в каждой семье родится 1,8 ребенка. Я предпочитаю термин средняя величина в долгосрочной перспективе : вы получите такую сумму за каждый билет, если будете играть в лотерею снова, и снова, и снова, и снова, и снова…

Разумеется, 30 центов — это меньше, чем вы потратили, но, хотя развлечение не бесплатное, Заядлый Игрок готов пойти на риск. Опросите американцев, зачем они играют в лотерею, и половина скажет: не ради денег, а ради удовольствия [77] Charles Clotfelter and Philip Cook, «On the Economics of State Lotteries», Journal of Economic Perspectives 4, no. 4 (Autumn 1990): 105–19, http://www.walkerd.people.cofc.edu/360/AcademicArticles/ClotfelterCookLottery.pdf . .

Таковы Заядлые Игроки. Поэтому, когда государство запускает новый вид лотереи, общие продажи лотерейных билетов растут [78] Kent Grote and Victor Matheson, «The Economics of Lotteries: A Survey of the Literature», College of the Holy Cross, Department of Economics Faculty Research Series, Paper No. 11–09, August 2011, http://college.holycross.edu/RePEc/hcx/Grote-Matheson_LiteratureReview.pdf . Пользуясь случаем, я хочу выразить огромную признательность Виктору Мэтисону, за то что он нашел время посмотреть черновик этой главы. . Заядлые Игроки видят в новых лотереях не альтернативные возможности инвестиций (что привело бы, соответственно, к падению продаж билетов старой лотереи), а новые развлечения, что-то вроде свежих фильмов в мультиплексе.