Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Что именно привлекает Заядлого Игрока? Радость победы, прилив адреналина от непредсказуемости, приятное волнение от наблюдения за развитием событий? Ну, это зависит от аппетитов конкретного Заядлого Игрока.

Я могу сказать наверняка, к чему он не стремится: к финансовой выгоде. В долгосрочной перспективе покупка лотерейного билета почти всегда означает потерю денег, а не прибыль.

Погодите… Почти всегда? Как это «почти»? Какое правительство настолько тупоумно, что продает лотерейные билеты себе в убыток?

Эти исключения возникают из общего правила, согласно которому лотереи с большим джекпотом подслащивают сделку: если никто не выигрывает джекпот на этой неделе, он пополняет призовой фонд на следующей неделе, и в итоге наибольший выигрыш увеличивается. Если это повторяется несколько раз, ожидаемый выигрыш одного билета начинает превышать его стоимость. Например, в январе 2016 года Национальная лотерея Великобритании предложила лакомый ожидаемый выигрыш более четырех фунтов стерлингов при стоимости билета два фунта [79] Alex Bellos, «There’s Never Been a Better Day to Play the Lottery, Mathematically Speaking», Guardian, January 9, 2016, https://www.theguardian.com/science/2016/jan/09/national-lottery-lotto-drawing-odds-of-winning-maths . . Как ни странно, такие схемы обычно стимулируют более чем достаточно продаж, чтобы оправдать затраты.

В очереди за лотерейным билетом наподобие этого вы встретите очень необычного игрока — лакомство для таких азартных орнитологов, как мы. Видите, как он чистит перышки вон там, высоко в ветвях? Это Образованный Дурак — редкостный олух, который трактует ожидаемый выигрыш, пользуясь плодами образования, как все глупые люди: путает частичную истину и универсальную мудрость.

Ожидаемый выигрыш дистиллирует многогранность покупки лотерейного билета, со всеми возможными призами и вероятностями, до одного обобщающего числа. Это мощный ход. Кроме того, это упрощение.

Возьмем для примера два билета стоимостью один доллар.

Потратьте $10 млн на билеты категории A, и вы получите $9 млн, то есть ожидаемый убыток при покупке каждого билета составляет 10 центов. В то же время $10 млн, потраченных на билеты категории B, принесут вам $11 млн и на сей раз ожидаемая прибыль от каждого билета составляет 10 центов. Таким образом, для тех, кто влюблен в ожидаемый выигрыш, вторая категория билетов кажется настоящим золотом, а первая — кошачьим {41} 41 «Кошачье золото», «золото для дураков» — дешевый минерал пирит, внешне напоминающий золото. — Прим. пер. .

И все же… принесут ли мне $11 млн больше счастья, чем $9 млн? Обе суммы во много раз превышают мой текущий счет в банке. Психологическая разница незначительна. Так зачем же называть одно мошенничеством, а другое отличной сделкой?

Если упростить: представьте, что Билл Гейтс предлагает вам пари. За один доллар вы с шансом 1 к 1 000 000 000 получаете $10 млрд. Посчитав ожидаемый выигрыш, вы пускаете слюни: миллиард, потраченный на лотерейные билеты, обеспечит вам выигрыш $10 млрд. Невозможно удержаться!

Но даже в этом случае, Образованный Дурак, я прошу вас удержаться. Вы не можете позволить себе эту игру. Наскребите впечатляющий миллион долларов, и все равно богатый человек Гейтс с вероятностью 99 % станет на один миллион богаче, а вы на один миллион беднее. Ожидаемый выигрыш — это средняя величина в долгосрочной перспективе, и, отозвавшись на предложение Билла Гейтса, вы исчерпаете свои финансы раньше, чем эта долгосрочная перспектива наступит.

То же самое верно по отношению к большинству лотерей. Возможно, вы окончательно разуверитесь в ожидаемом выигрыше, ознакомившись с такими абстрактными возможностями однодолларового лотерейного билета:

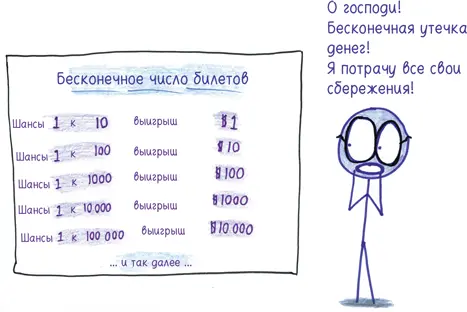
Если вы купите десять билетов, вы, скорее всего, выиграете один доллар. В общем-то, ужасно: 10 центов за каждый билет.

Если вы купите 100 билетов, вы, скорее всего, выиграете $20. (Десять самых маленьких призов и один приз в $10.) Чуть менее ужасно: 20 центов за билет.

Если вы купите 1000 билетов, то, скорее всего, вы выиграете $300. (Сто призов по одному доллару, десять призов по $10 и один приз в $100.) Вы получите по 30 центов с каждого билета.

Продолжаем. Чем больше билетов вы купите, тем больший выигрыш вы можете ожидать. Если вы каким-то образом умудритесь купить миллиард билетов, скорее всего, на каждый билет вы выиграете $1,2. Квадриллион билетов? Еще лучше: $1,5 на билет. Действительно, чем больше у вас билетов, тем больше будет ваша прибыль от каждого билета. Если вы каким-то образом сможете инвестировать гугол долларов, вы получите десять гуголов взамен. Любая желаемая выручка — надо просто накупить достаточное количество билетов. Ожидаемая прибыль от одного билета бесконечна.

Но даже если вы доверяете правительству, затеявшему такую лотерею, вы никогда не сможете позволить себе купить достаточное количество билетов, чтобы увидеть хотя бы отблеск бесконечной прибыли. Идите и потратьте всю свою жизнь на покупку билетов, Образованный Дурак. С ошеломляющей вероятностью вас ждет банкротство.

Мы, люди, — создания кратковременные. Лучше оставим бессмертным среднюю величину в долгосрочной перспективе.

О, посмотрите-ка, кто только что занял очередь. Это Мальчик на побегушках!

В отличие от большинства стоящих в этой очереди, заработок Мальчика на побегушках гарантирован. Дело в том, что Мальчик на побегушках покупает билеты не для себя: просто отстаивает очередь, тратит некую сумму, покупает билеты и передает заказчику. Компенсация скромная, однако надежная.

Кто заплатит Мальчику на побегушках? Ну, это вопрос к нашему следующему игроку…

На первый взгляд этот персонаж ужасно похож на Образованного Дурака: тот же сверкающий взгляд, та же одержимость ожидаемым выигрышем. Но поглядите-ка, что происходит, когда он обнаруживает лотерею, у которой ожидаемый выигрыш положителен {42} 42 Точнее, положительна ожидаемая прибыль: это ожидаемый выигрыш минус расходы на приобретение билетов. — Прим. науч. ред . . В то время как Образованный Дурак размахивает руками, покупает горемычную горсть билетов и редко выигрывает, Крупный Игрок втайне осуществляет простой и гнусный план. Чтобы преодолеть риск, вам недостаточно купить всего несколько билетов. Вы должны выкупить все.