Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

И это далеко не все. Статистика классифицирует, экстраполирует и прогнозирует, позволяя нам выстраивать эффективные модели реальности. Да, весь этот процесс основан на упрощениях. И да, упрощение — это обман через умалчивание. Но в лучших проявлениях статистика — честная разновидность лжи. Этот процесс взывает к самым благородным атрибутам человеческой мысли, от любознательности до милосердия.

В этом плане статистика не так уж отличается от схематичных человечков. Это дурацкие рисунки, где нет ладоней и носов, и все же по-своему они правдивы.

Окей, давайте взглянем непредвзято. Статистика — это ложь. Ей нельзя доверять. Так говорили все умнейшие люди в истории. Или нет?

К чему я клоню? Да, цифры могут лгать. Но и слова тоже — не говоря уже о картинах, жестах, хип-хоп-мюзиклах и электронных рассылках с просьбами о фандрайзинге. Наша система морали обвиняет обманщика, а не средство обмана. На мой взгляд, самые интересные критические высказывания в адрес статистики касаются не подлости статистиков, а самой математики. Мы можем повысить ценность статистики, понимая ее несовершенства, осознавая, какую цель преследует тот или иной статистический анализ — и что он намеренно оставляет за скобками. Может быть, тогда мы сможем стать ответственными гражданами, о которых мечтал Герберт Уэллс [143].

Как вычислить?Сложите все величины, которые у вас есть. Затем разделите эту сумму на количество величин.

Когда использовать?Среднее арифметическое (или среднее значение, как часто говорят) удовлетворяет основной потребности статистики: уловить центральную тенденцию совокупности величин. Каков средний рост игрока баскетбольной команды? Сколько рожков мороженого вы продаете в день? Насколько весь класс справился с контрольной работой? Если вы хотите охарактеризовать совокупность величин одним числом, то разумно в первую очередь начать со среднего арифметического.

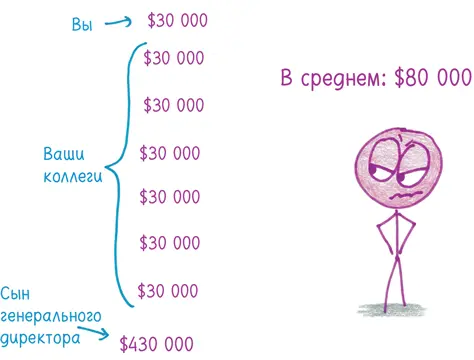
Почему нельзя доверять?Среднее арифметическое учитывает лишь два показателя: общую сумму и количество людей, внесших свою лепту.

Если вы когда-нибудь делили пиратский клад, то осознаете опасность: есть много способов делить добычу. Сколько получает каждый? Что мы видим: баланс или перевес в чью-то пользу? Если я умял всю пиццу и ничего вам не оставил, насколько честно говорить, что в среднем мы съели по полпиццы? Вы можете сказать гостям за ужином, что у среднестатистического человека один яичник и одно яичко, но следом, возможно, повиснет неловкая пауза. (Я пробовал; так и произошло.)

Людей волнуют вопросы распределения ресурсов. Вычисляя среднее арифметическое, мы закрываем на них глаза.

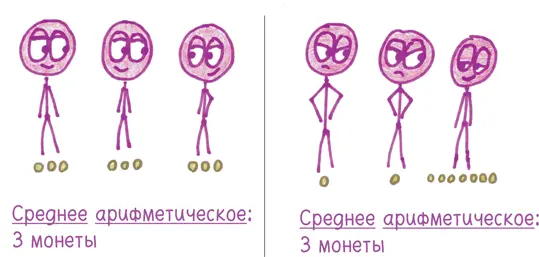
Спасительная благодать заключается в том, что эта особенность упрощает вычисления. Скажем, вы сдали экзамены на 87, 88 и 96 баллов. (Да, вы царь горы в этом классе.) Чему равен ваш средний балл? Не перегревайте нейроны сложением и делением; просто перегруппируйте величины. Отнимите шесть баллов от последней оценки; прибавьте три балла к первой и два — ко второй. Теперь ваши оценки равны 90, 90, 90 плюс один дополнительный балл. Поделите этот балл на три, и, не перенапрягая извилины, вычислите свою среднюю оценку: 90⅓.

Как вычислить?Упорядочите ваши величины по возрастанию и возьмите средний элемент. Ровно половина величин будет меньше, ровно половина — больше {60} .

Когда использовать?Медиана, как и среднее арифметическое, характеризует центральную тенденцию совокупности величин. Разница в ее чувствительности к отклонениям — или скорее не чувствительности.

Возьмем, к примеру, семейный заработок [144]. В США богатая семья может зарабатывать в десятки (даже в сотни) раз больше, чем бедная. Вычисляя среднее арифметическое, мы исходим из того, что каждой семье достается равная доля совокупных доходов, и впадаем в искушение закрыть глаза на разброс величин и оказаться далеко от основного объема значений. В среднем семейный доход в США составляет около $75 000.

Медиана не поддается притяжению крупных величин. Вместо этого она показывает идеальную среднюю точку, доход семьи, которая богаче половины американских семей и беднее другой половины. В США это около $58 000. В отличие от среднего арифметического, это число дает ясную картину среднестатистической семьи.

Почему нельзя доверять?Вычислив медиану, вы знаете, что половина данных больше, а половина меньше. Но насколько далеко отстоят эти точки? На толщину волоса или на длину трансконтинентального полета? Вы видите только один кусок пирога, не понимая, насколько велики или малы другие. Это может ввести в заблуждение.

Когда венчурный капиталист инвестирует в новые фирмы, он исходит из того, что по большей части все они прогорят. Одно попадание в яблочко из десяти компенсирует все мелкие потери. Но медиана не учитывает эту динамику. «Типичный исход отрицательный, — вопит она. — Отменяем миссию!»

В то же время страховая компания тщательно наполняет портфель, зная, что стихийное бедствие с вероятностью 1 к 1000 сведет на нет всю скромную прибыль, накопленную за годы. Но медиана не учитывает потенциальную опасность. «Эй, типичный результат положительный, — подбадривает она. — Полный вперед!»

Вот почему вместе со средним арифметическим часто указывают медиану. Медиана рапортует о типичной величине; среднее арифметическое — обо всей совокупности величин. Они словно два ненадежных свидетеля: по отдельности их рассказы неполны, но, выслушав их вместе, мы можем восстановить более цельную картину.