Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Хаос учит смирению. Он вновь и вновь очерчивает границы нашего познания.

В 1967 году легендарный авантюрист и математик хаоса Бенуа Мандельброт опубликовал короткую сенсационную статью под названием «Какова длина побережья Британии?» [267]. Проблема сложнее, чем кажется на первый взгляд, потому что — как ни странно — длина побережья Британии зависит от того, каким образом его измерять.

Для начала возьмите линейку длиной 10 км, и вы получите определенную длину. Затем увеличьте масштаб и возьмите линейку в 1 км. Участки, которые раньше казались прямыми, при ближайшем рассмотрении оказываются довольно извилистыми. С помощью более точной линейки вы сможете учесть бухты и мысы, которые не принимали во внимание раньше, и общая длина возрастет.

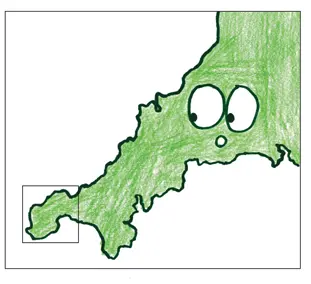
Мы еще не закончили. Возьмите стометровую линейку, и процесс повторится. Становятся видны кривизны и изгибы, которые были незаметны раньше, и вносят в общую длину свой вклад.

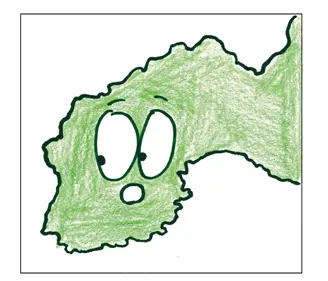
Мы можем повторять процесс снова и снова. Чем точнее измерения, тем длиннее становится береговая линия, — теоретически мы можем продолжать до бесконечности.

Мягко говоря, это довольно странно. В большинстве исследований более пристальный взгляд помогает прояснить ответ. Здесь все пугающе наоборот: более пристальный взгляд лишь запутывает дело. Оно никогда не упрощается, никогда не решается.

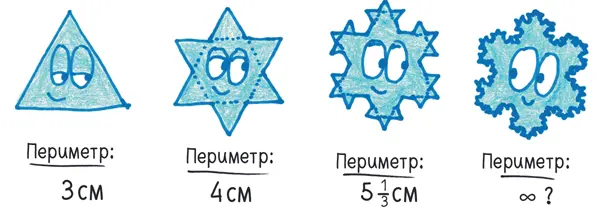
Эта схема достигает своего предела в случае снежинки Коха — математического объекта, состоящего из нагромождения зубцов на зубцах на зубцах. Хотя на этой странице она занимает мало места, длина ее границы теоретически бесконечна.

В графическом романе «Из ада», где в жанре альтернативной истории рассказано о серии убийств в лондонском районе Уайтчепел в 1888 году, писатель Алан Мур уподобляет изучение истории снежинке Коха. «Всякая новая книга, — говорит он в послесловии, — содержит новые детали, более мелкие зубцы на границе фигуры. Однако она не выходит за пределы очерченного круга: осень 1888 года, Уайтчепел» [268].

По мнению Мура, изучение истории по-своему бездонно [269]. Чем пристальней мы всматриваемся, тем больше видим. Конечный фрагмент пространственно-временного континуума может заключать в себе бесчисленные слои деталей, позволяющих выстраивать причинно-следственные цепочки анализа до бесконечности. Хаос порождает сложности на протяжении всего пути, картина никогда не распадается на пиксели, расследование не заканчивается, дело не упрощается.

Так что же, история хаотична, как игра «Жизнь» — простая в малом масштабе, но непредсказуемая в большом? Или она непредсказуема, как погода, — своевольные каждодневные колебания усредняются в долгосрочной перспективе, и в целом климат довольно стабилен? Или, может быть, она похожа на снежинку Коха — хаос на каждом уровне, сложность в любом масштабе? Эти три метафоры борются в моем сознании, словно три презентации в PowerPoint, спроецированные на один экран [270]. Иногда мне кажется, что я уже на грани понимания, — но вот я заглядываю в ленту новостей, и мир вновь преображается, принимая новый облик, странный и непостижимый.

Элементы этой книги немного похожи на атомы моего тела: они лишь номинально и временно «мои». Они бродили во мне на протяжении многих лет; их источников слишком много, чтобы отследить все или воздать им должное. Лучшее, что я могу сделать, — просто указать на общую экосистему, которая сделала эту книгу возможной.

За стиль этой книги я благодарен всем остроумным и добросердечным сотрудникам Yale Records {85} ; прежде всего я снимаю шляпу перед Дэвидом Клампом и Дэвидом Литтом, Михаэлем Гербером и Михаэлем Торнтоном.

Ракурс для этой книги я нашел благодаря моим выдающимся коллегам в школе имени Короля Эдуарда {86} , особенно благодаря вам, Том, Эд, Джеймс, Кэз, Ричард, Ней… Да чего уж там, черт возьми, благодаря вам всем. Учителя — шутливый, въедливый, разносторонний, любознательный и слегка сумасшедший народ, и я горжусь тем, что я к нему принадлежу.

За понимание цели этой книги я благодарен моим ученикам и моим учителям, которые бессчетными (ℵ 1) {87} способами сформировали мое представление о математике и мире.

Я заранее приношу извинения за все ошибки, допущенные в этой книге (особенно за все прозеванные благодарности).

За сам факт существования этой книги я благодарю: десятки любезных коллег и друзей, которые высказывали комментарии и советы (см. примечания); Чэнка Дизеля — за то, что он изящно превратил мои каракули в нечто удобочитаемое; Майка Оливо — за то, что просветил меня по поводу вуки; Пола Кеппла — за то, что он собрал прорву никудышных рисунков в единое целое, и оно стало прекрасным; Элизабет Джонсон — за то, что она выступила миротворцем в омерзительном побоище между мною и дефисами и знает, сколько букв «е» должно быть в слове «Че-е-е-е-ерт!»; Бетси Халсебош, Кару Томсон и других сотрудников издательства Dog & Leventhal ; Дадо Дервискадика и Стива Троха — за то, что они увидели прообраз этой книги (за целую вечность до того, как его смог увидеть я) и помогли мне дойти до финала; и Бекки Кох — за блестящую редактуру (похоже, эта профессия требует изощреннейших навыков одновременно исполнительного продюсера и воспитателя детей).

Передаю слова любви и благодарности моей семье: Джиму, Дженну, Кэролайн, Ларку, Фариду, Джастину, Диане, Карлу, моему счастливому треугольнику Сорайе, моему картофельному кудеснику Скандеру, Пегги, Полу, Кайе и кланам Орлинов, Хоганов и Уильямсов во всей их полноте. Я храню теплые воспоминания об Алдене, Роз, Полине и, конечно же, Донне.

И наконец: спасибо, Тэрин. Ты выбрала математику, и я рад, что мы отправились в это путешествие вдвоем. Я люблю тебя даже сильнее, чем я тебя троллю.

Термин теории игр. Выигрыш одного игрока равен проигрышу другого. Простейший пример — игра в орлянку. Строго говоря, уроки математики не являются такой игрой: все ученики могут одновременно получить высший балл и «выиграть» (или наоборот), хотя, конечно, это крайне маловероятно. — Прим. пер.