Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]

Важным является то, что элемент обеспечивает размерами условие сплошности. Это требует, чтобы размеры были намного больше размеров молекул, кристаллических структур и даже зерен (для стали), на уровне которых существует не сплошность.

Элемент не может быть «стянут» в точку и для него существует минимальные размеры, меньше которых элемент быть не может.

Покажем условия равновесия на основании тетраэдра, описанного вокруг интересующей точки. Процитируем графику Новожилова [3,с.14]:

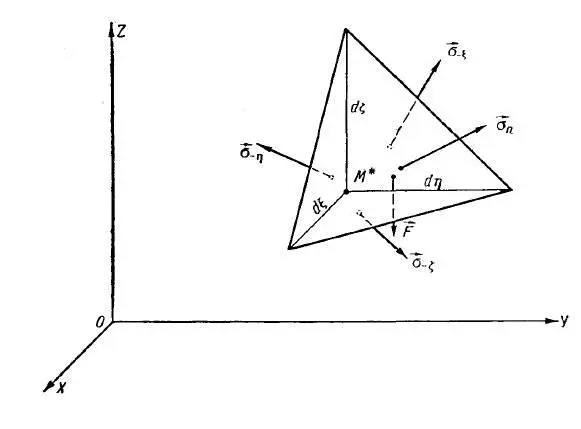
и соответствующий этой графике вид «в плане», наглядно показывающий необходимость касательных напряжений для условий равновесия [3], но также необходимых для препятствия вырыва элемента из стенки оболочки вдоль меридиональных и кольцевых секущих плоскостей:

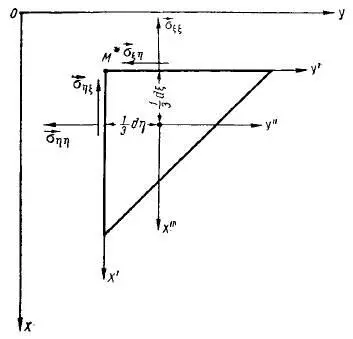
После совмещения

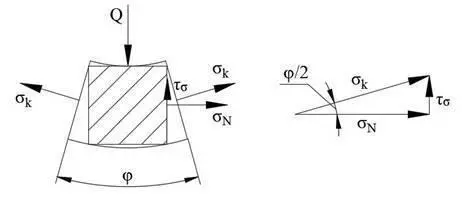
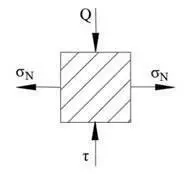
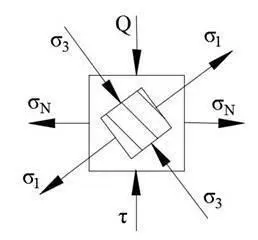
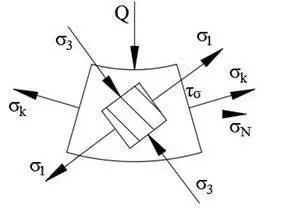
Из приведенной графики отчетливо видно, что главные напряжения не являются кольцевыми напряжениями (не совпадают по направлению).

Очевидно, что необходимо в точке совмещения перейти от кольцевых и меридиональных напряжений к главным напряжениям и условия равенства площадей верхних и боковых граней кольцевого сегмента не выполняются.

Итак, рассмотрев осесимметричную задачу теории упругости, на основании простых геометрических соображений и распределения напряжений вокруг точки тела, положенных в основание теории упругости, можно сделать вывод о некорректности осесимметричной задачи, об ошибке в этой задаче.

По мнению автора, осесимметричная задача в существующем виде должна быть признана некорректной и доработана с учетом написанного выше.

Трехмерная задача теории упругости построена корректно. Оболочка рассматривается как твердое тело, к которому непосредственно прикладывают нагрузки и изучают вызванные деформации и напряжения.

Ниже более подробно рассмотрим применение трехмерной и осесимметричной задач к расчету оболочек корпуса нефтяных и атомных аппаратов.

Затем приведем формулы с обоснованием, используемые в нормах для сосудов высокого давления до 130 МПа и оценку прочности стенки сосудов.

Трехмерная задача для оболочек цилиндра (задача Ламе) и сферы подробно решена в работе член.-корр. Лурье А.И. [6,с.387].

Лурье А.И. записал краевые условия (давления приняты одинаковыми) [6]:

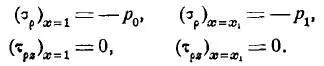
По краевым условиям находятся постоянные интегрирования уравнений [6]:

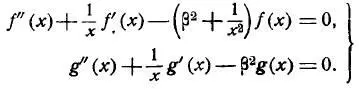
Эти уравнения выведены из уравнений перемещения точек упругого тела в осесимметричной задаче, записанного в цилиндрических координатах ( как было написано выше, оболочка рассматривается в виде твердого тела и к ней непосредственно прикладываются нагрузки и изучаются деформации и напряжения ) [6]:

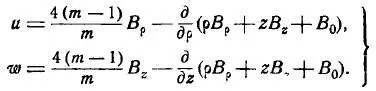
U – радиальное перемещение, w – осевое перемещение. Расшифровка остальных членов – см. работу [6,с.384].

Для напряжений по закону Гука, Лурье записал [6]:

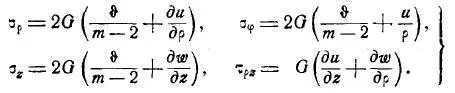
После выполнения выкладок по краевым условиям, записанным выше, Лурье получает уравнения для цилиндра в задаче Ламе для деформаций (перемещений) и напряжений.

Для деформаций цилиндра без продольного перемещения торцов [6]:

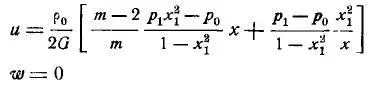
Для напряжений цилиндра без продольного перемещения торцов [6]:

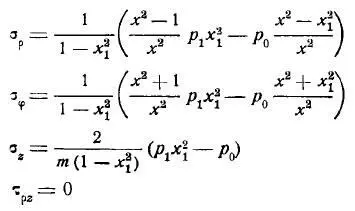
Для деформаций цилиндра со свободным перемещения торцов [6]:

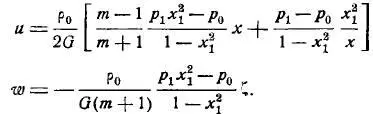
Для напряжений цилиндра со свободным перемещения торцов [6]:

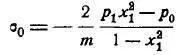
Для деформаций цилиндра под наружным давлением со свободным перемещения торцов [6]:

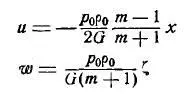
Для напряжений цилиндра под наружным давлением со свободным перемещения торцов [6]:

На основании приведенных выше формул можно выполнять расчет аппаратов высокого давления до 130МПа по трехмерной задаче теории упругости.

В настоящее время расчет оболочек аппаратов в виде трехмерного твердого тела с определением напряжений и деформаций выполняется методом конечных элементов (МКЭ) в специальных программных пакетах, например, ANSYS

Повторно процитируем графику из работы Безухова [2,с.143]:

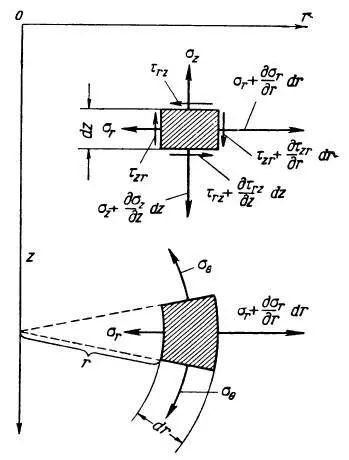
Уравнения равновесия [2]:

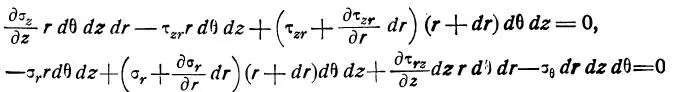
После преобразований [2]:

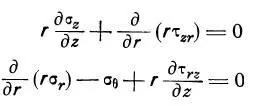
Уравнения для деформаций [2]:

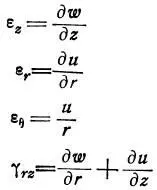
Уравнения для напряжений [2]:

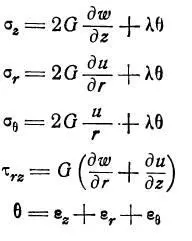
Объемное расширение тела [2]: