Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]
- Название:Теория расчета нефтяных аппаратов высокого давления [litres самиздат]
- Автор:
- Жанр:
- Издательство:Array SelfPub.ru
- Год:2021
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат] краткое содержание
Теория расчета нефтяных аппаратов высокого давления [litres самиздат] - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Векторы напряжений и деформаций и матрица упругости по данным [15,с.229]:

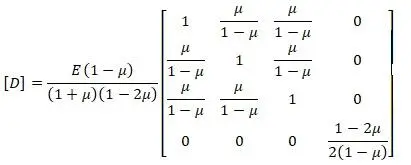
Вектор начальной деформации от теплового воздействия [15,с.230]:
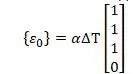
Напряжения вычисляются по закону Гука [15,с.233]:
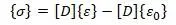
или через узловые перемещения после подстановки
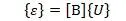
([В] – матрица градиента, {U} – перемещение узлов.

В работе [14,с.259] отмечено о применении одномерных элементов для осесимметричных оболочек к осесимметричной нагрузкой. В этом случае используется метод перемещений и поверхность оболочки разбивается на ряд усеченных конусов:
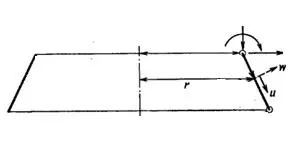
Изгибные и мембранные напряжения в оболочке корпуса аппарата однозначно определяются величинами обобщенными деформациями (искривления и растяжения срединной поверхности) [14,с.259]. Перемещения каждой точки срединной поверхности известны. Так, перемещения срединной поверхности оболочки под действием осесимметричной нагрузки однозначно определяются компонентами u и w по касательной к нормали поверхности.
Зенковичем [14,с.259] приводится следующая запись матриц перемещений {ε}, напряжений {σ} и упругости [D] в соответствии с четырьмя результирующими напряжениями на рисунке при φ = const (верхняя часть матриц соответствует мембранным усилиям, нижняя часть матриц соответствует изгибным жесткостям, сдвиговые части матриц не показаны):

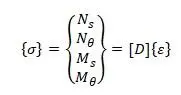
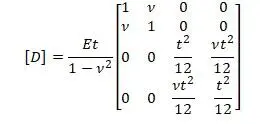
Расчет колебаний аппаратов
Для решения задач колебаний колонных аппаратов необходимо учитывать зависимость изменения рассчитываемых параметров во времени.
Используется эквивалентная статическая задача, в которой каждый момент времени дискретизируется. Распределенная сила может быть заменена эквивалентной.
Для оболочек, как отмечает Зенкевич [16,с.352], записывается матрица масс конечных элементов (для плоских и изгибных напряжений), по которой находится общая матрица масс. Матрица масс строится аналогично матрице жесткости. Зенкевич на этом основании заключает, что решение задачи о колебаниях оболочек не вызывает затруднений.
В работе [16,с.176] Зенкевич отмечает, что введение инерционных членов в статическую задачу не усложняет решения. После вычисления матрицы масс элементов, задача принимает вид стандартной системы с конечным числом степеней свободы.
Для оболочки, совершающей перемещения (движение) динамическая задачи переводится в статическую задачу приложением сил от ускорения (по принципу д’Аламбера).
В работе [16,с.176] показано, что расчет упругой конструкции в условиях статической нагрузки описывается уравнением:
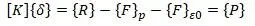
В этом уравнении [K] – матрица жесткости объединенной конструкции, {δ} – матрица всех узловых смещений, {Р} – матрица всех узловых нагрузок.
{F}p – силы в узлах от распределенных нагрузок, см. [38,с.176],
{F}ε0 – силы в узлах от начальной деформации, см. [38,с.21].
Матрица динамических сил в узлах [16,с.176]:
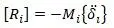
Матрица распределенной нагрузки [16,с.177]:
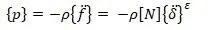
Распределенная нагрузка выражается в виде эквивалентных узловых сил [16,с.177]:
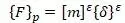
После подстановки в первоначальное уравнение [16,с.177]:
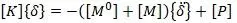
Матрица внешних масс, прикладываемых к узлам сетки [16,с.177]:
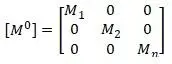
Матрица масс, объединяющая матрицы масс конечных элементов [16,с.177]:

Для колебаний с затуханием первоначальное уравнение записывается в виде [16,с.186]
([С] – матрица затухания колебаний)
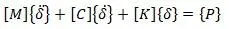
Матрица затухания колебаний [С] находится аналогично матрице масс [М].
Для внешней силы можно записать [16,с.186]:
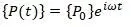
C учетом этой записи получается форма решения в виде [16,с.186]:

Первоначальное уравнение, решенное относительно {δ0} [16,с.186]:
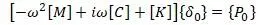
Из последнего уравнения записывается система двух уравнений [16,с.187]:
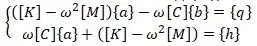
с учетом записи {δ0} является комплексным и [16,с.186]:

Реакция конструкции с затуханием колебаний на периодическое воздействие силы с угловой частотой ω находится решением системы уравнений [16,с.187].
Получение n собственных величин и {δ’0}I собственных форм колебаний получается решением уравнения [16,с.178]:
Читать дальшеИнтервал:
Закладка:
![Обложка книги Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]](/books/1149602/konstantin-efanov-teoriya-rascheta-neftyanyh-apparato.webp)