Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]
- Название:Теория расчета нефтяных аппаратов высокого давления [litres самиздат]
- Автор:
- Жанр:
- Издательство:Array SelfPub.ru
- Год:2021
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат] краткое содержание
Теория расчета нефтяных аппаратов высокого давления [litres самиздат] - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Вихманом и Кругловым [11,с.148] получены результаты:
– для тонкостенных сосудов
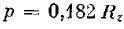
– по третьей теории прочности:

– по четвертой теории прочности:
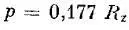
Авторы [10] сделали вывод о том, что для тонкостенных сосудов с отношением толщины стенки к диаметру менее 0,1, результаты по формулам для толстостенных и тонкостенных сосудов приближенно одинаковые.
Таким образом, приведенный вывод авторов [10] соответствует указанной выше автором настоящей монографии положению об универсальности теории упругости и возможности расчета по методике аппаратов высокого давления для аппаратов до 21МПа. И о возможности на давление до 21МПа проектирования и изготовления аппаратов по нормам на аппараты высокого давления до 130 МПа, работающие в интервале «вакуум – 130 МПа», перекрывающем интервал «вакуум – 21 МПа».
При гидроиспытаниях, как указано в [11] с коэффициентом 1,25, напряжения на внутренней поверхности составляют 0,9 от предела текучести.
Также в работе [11] указан коэффициент, равный 0,136 отношения толщины стенки к внутреннему диаметру, при котором напряжения на внутренней поверхности оболочки достигают 0,9 от предела текучести (осредненные напряжения по теории тонких оболочек 0,58 от предела текучести и тангенциальные напряжения 0,72 от предела текучести).
И в работе [11] в итоге указана формула для толстостенных сосудов из аустенитно-ферритной стали по Фрейтагу В.А.:
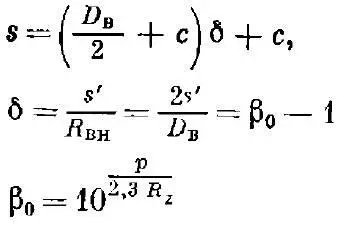
Расчет методом конечных элементов
Приведем пример реализации решения численным методом – методом конечных элементов трехмерной и осесимметричной задач теории упругости.
В настоящее время расчеты МКИ проводят в программном пакете МКЭ, например, ANSYS, рассчитывая корпус аппарата полностью в сборе на комбинацию всех видов нагрузки.
Результатом расчета являются цветные диаграммы деформаций и напряжений, по которым делается заключение о работоспособности конструкции аппарата для заданных расчетных нагрузок.
Под расчетом по методу конечных элементов понимается вычислительный процесс на компьютере, состоящий из [13,с.6]:
– описания конечных элементов, численного интегрирования для вычисления элементов матриц,
– объединение матриц отдельных конечных элементов в общую матрицу ансамбля элементов,
– численное решение системы уравнений равновесия.
Решение уравнений равновесия для статических и динамических задач занимает основные затраты машинного времени на вычисления. Инженер-расчетчик может контролировать ход вычисления.
При расчете МКЭ оболочек (т.е. корпусов аппаратов) предполагается [13,с.73], связь конечных элементов в узловых точек (которых конечное число), перемещения узловых точек определяют перемещения конечных элементов (поля конечных элементов). За счет этого используя принцип возможных перемещений можно составить уравнения равновесия для совокупности всех конечных элементов.
Решение
трехмерной задачи теории упругости
Приведем пример формы трехмерного конечного элемента:
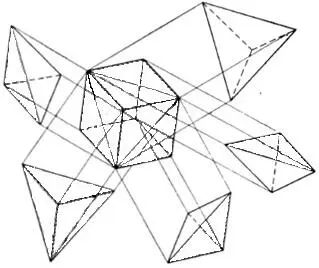
Перемещения тетраэдрического элемента определяется перемещением 12 компонентами перемещений его узлов [14,с.107]:
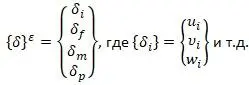
Компонентами u, v, w определяется вектор перемещений точки.
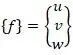
Матрица деформаций [14,с.108]:
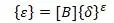
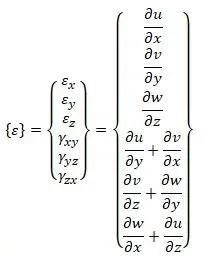
Матрица тепловых деформаций [14,с.109] (θε – средняя температура элемента):
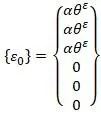
Матрица упругости [14,с.109]:

Матрица напряжений [14,с.109] ({σ0 – аддитивный член}):

Объединяя тетраэдрические элементы, можно разбивать пространство на «кирпичики». В этом случае повышается наглядность разбиения.
Зенкевич указывает [14,с.115] о расчете сосуда высокого давления МКЭ с использованием конечных элементов в виде «кирпичиков». В приводимом примере расчета выполнялся для 10000 степеней свободы. И Зенкевич указывает на то, что при применении более сложных конечных элементов расчет упрощается за счет уменьшения степеней свободы. Но использование сложных элементов не даст преимуществ в сокращении времени подготовки расчета, если процесс разбиения автоматизирован [14,с.169]. В настоящее время в программных пакетах МКЭ используется автоматизированное построение расчетной сетки. При этом при применении сложных элементов сокращается время вычислений, однако ширина матрицы увеличивается и сокращение времени может не происходить. Увеличение размеров конечных элементов приводит к ухудшению аппроксимации конструкции.
Решение осесимметричной задачи теории упругости
По данным [14,с.89] , [15,с.229] для решения осесимметричной задачи может быть использован подход плоской задачи. В этом случае треугольный симплекс-элемент вращением образует треугольный тор [15,с.229]. Такой тор показан на рисунке в работе О. Зенкевича [14,с.87]
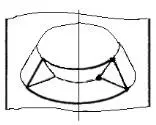
Объемное тело 3D-модели представляет собой объем, по которому берется интеграл таких треугольных элементов. Отличие осесимметричной задачи от плоской состоит в том, что при деформации оболочки в радиальном направлении вызывает деформацию в окружном направлении. И в рассмотрение должна быть введена четвертая компонента деформации и напряжения по сравнению со случаем плоской задачи [14,с.88]. В плоской задаче компоненты напряжения в направлении, перпендикулярном к координатной плоскости, равны нулю. Трехмерный симплекс-элемент рассматривается аналогично двумерному конечному элементу [15,с.226].
Читать дальшеИнтервал:
Закладка:
![Обложка книги Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]](/books/1149602/konstantin-efanov-teoriya-rascheta-neftyanyh-apparato.webp)