Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]

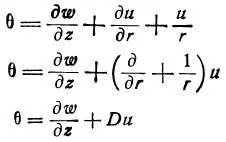
Перемещения должны описываться уравнениями [2]:

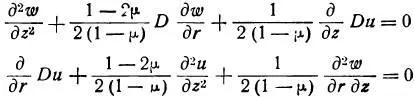
Для поиска напряжений, уравнения напряжений теории упругости преобразуют из прямоугольных (декартовых) в цилиндрические координаты.

Записывают уравнение [2]:

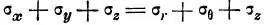
После выкладок получается [2]:

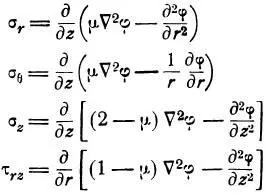
При подстановки записанных уравнений для напряжений в записанные выше уравнения статического равновесия выделенного элемента, последние обращаются в тождества [2].

Безухов [2,с.180] при рассмотрении задачи Ламе записывает граничные условия и ссылается на формулы для плоской задачи теории упругости [2,с.138], полученные для напряжений, распределенных симметрично относительно оси. Процитируем графику для плоской задачи [2,с.136]:

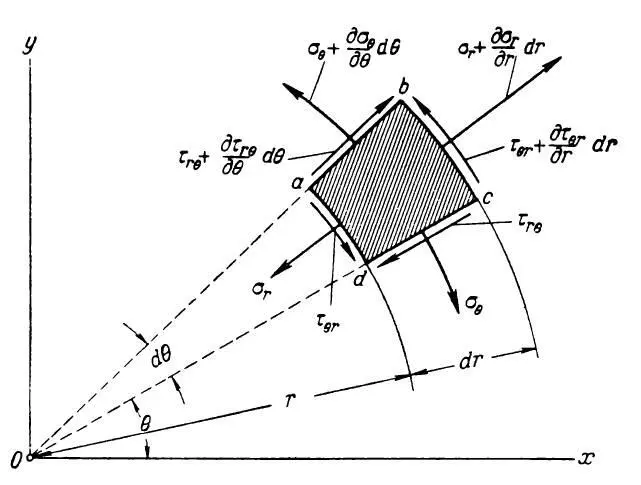
Для этой графики Безухов некорректно указывает, что касательные напряжения по определенным граням равны нулю. На некорректность этого утверждения для случая осесимметричной задачи аргументы были приведены выше автором настоящей работы.

Безухов записывает формулы для напряжений [2]:

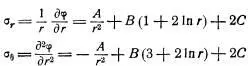
Из этих уравнений, приняв В = 0, получается [2,с.180]:

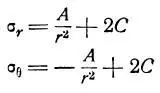
Из граничных условий

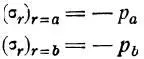
получается:

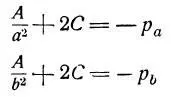
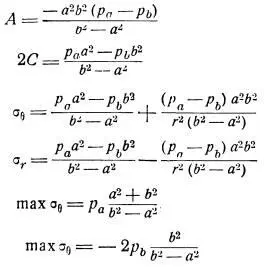
Результат в виде формул получился таким же как и в литературе по сопротивлению материалов, например, в учебниках Беляева Н.М. [6,с.609] и Ильюшина [7,с.176]. Но в сопротивлении материалов формулы выводятся по-другому. Особенностью изложения Беляевым является подчеркивание универсальности теории упругости и применение полученных формул для толстостенных сосудов к расчету тонкостенных сосудов.

Процитируем графику из работы Ильюшина [7,с.177]:

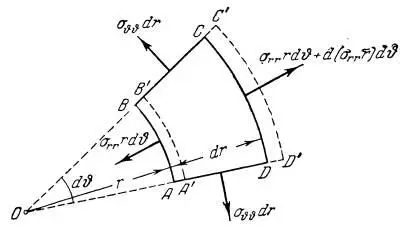
Ильюшин записывает известные уравнения [7,с.178]:

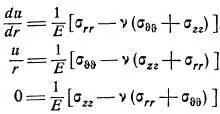
Уравнение равновесия [7,с.178]:

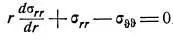
И затем после промежуточных выкладок находит три напряжения [7,с.179]:

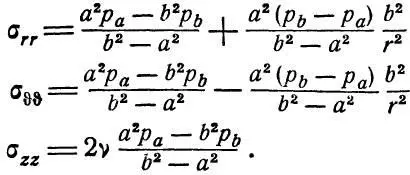
Как видно, формулы совпадают с полученными Безуховым, однако выведены другим путем.

Для случая пластического состояния материала стенки уравнение равновесия при внутреннем давлении Ильюшин записал [7,с.182]:

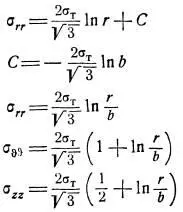
Формулы для деформаций и напряжений полой трубы при пластической деформации имеют более сложный вид, выводятся по-другому и приведены подробно в работе Ильюшина [8,с.144].

Папкович в работе [9] указывает, что для длинного цилиндра посередине будет плоское напряженное состояние. На этом основании, по-видимому, в литературе по теории упругости, например [2], при рассмотрении задачи Ламе производится рассмотрение плоской задачи и вывод формул по соответствующему пути. Несмотря на то, что в этой же литературе приведены формулы для осесимметричной задачи.

Такой подход является по существу некорректным. Необходимо применять трехмерную задачу, лишенную, по-видимому, указанных недостатков.

Меридиональные, радиальные, тангенциальные напряжения согласно работе [10,с.56]:

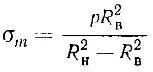
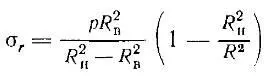
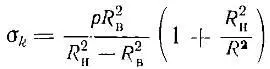
Как видно из записанных формул, величина радиальных и тангенциальных напряжений изменяется по толщине. Радиальное напряжение на внутренней поверхности стенки оболочки является равным внутреннему давлению. Тангенциальные напряжения на внутренней поверхности стенки достигают максимума.

Наибольшим напряжением будет являться тангенциальное при закрытых торцах цилиндра приваренными днищами [11,с.146]:

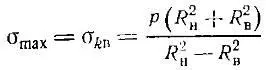
Рассмотрим оценку напряженного состояния по теориям прочности по данным работы [11].

По первой теории прочности [11,с.144]:

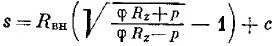
По второй теории прочности [11,с.145]:

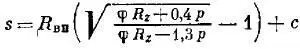
По третьей теории прочности [11,с.145]:

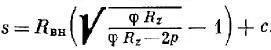
По четвертой теории прочности [11,с.145]:

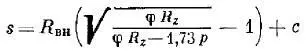
В работах [10] и [11] выполнено сравнение толщин стенок, рассчитанных по формулам теории упругости для толстостенных аппаратов и по формулам теории тонких оболочек для тонкостенных аппаратов. Сравнение выполнено для граничного условия отношения толщины стенки к диаметру, равному 0,1.

В теории тонких оболочек находят среднее напряжение аналогично теории пластин в виде интеграла, как показано в работе Новожилова [12]. По второй теории прочности для толстостенных сосудов применено формула для тонкостенных сосудов [11].