Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Я отдаю предпочтение задаче Уистона, в которой человек обходит земной шар, чем ее более поздней версии, где веревка парит над землей, поскольку, несмотря на очевидную абсурдность обеих ситуаций, первый сценарий кажется менее надуманным. Если бы такая веревка действительно существовала и вы бы удлинили ее на 1 метр, то, прежде чем думать о том, как поднять ее в воздух по всей длине, вы потянули бы веревку вверх в одной точке, чтобы посмотреть, на какую высоту она поднимется. Особенно если бы цель состояла в том, чтобы провести под веревкой какое-нибудь животное!

Новая задача

5. Допустим, у вас есть веревка, натянутая вокруг земного шара, и вы удлинили ее на 1 метр. Поднимайте веревку вверх в одной точке до тех пор, пока она не натянется. На какую высоту она поднялась? Какое животное сможет под ней пройти?

Не пытайтесь решить задачу, поскольку это по силам только людям с определенным уровнем математической подготовки. Я привел ее исключительно из-за оригинального решения. Попробуйте догадаться, как это делается, а затем сверьтесь с ответами в конце книги. Но сначала все же решите следующую задачу.

Подсказка: вам понадобится знание теоремы Пифагора, которая гласит, что во всех прямоугольных треугольниках квадрат гипотенузы равен сумме квадратов двух катетов. (Гипотенуза – это сторона, расположенная напротив прямого угла.) Но вы ведь это знаете, не так ли?

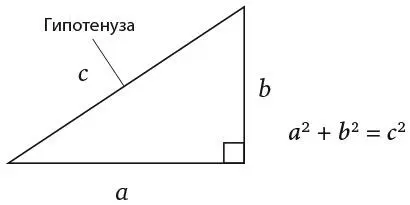
Ответ

На вашей улице длиной (от начала до конца) 100 метров будет проходить праздник. У вас есть 101-метровая гирлянда из флажков. Один ее конец вы прикрепляете к основанию фонарного столба в начале улицы, а другой – на расстоянии 100 метров у основания фонарного столба в конце улицы; середину гирлянды крепите к верхушке шеста, расположенного на полпути вниз по улице.

Какова высота шеста, если исходить из того, что гирлянда не провисает и не растягивается?

Следующие три головоломки касаются поведения катящихся кругов. Если вы никогда не размышляли над такими идеями, то ваша голова может пойти кругом. Однако я гарантирую, что ответы приведут вас в полный восторг. Вероятно, эти головоломки станут понятнее, если побывать в Японии.

«Начала» сделали Евклида выдающимся логиком, корифеем строгого дедуктивного мышления. Сегодня это звание разделяет, а может, даже затмевает Шерлок Холмс.

Вымышленный детектив стремился к евклидовой строгости («Сколько раз я говорил вам: “Отбросьте все невозможное, а то, что останется, и будет ответом, каким бы невероятным он ни казался”?»), но не был столь же силен в математике.

В одном из первых дел Шерлока Холмса под названием «Случай в интернате», изучив отпечатки велосипедных шин, сыщик делает вывод о том, куда направился велосипед. Он объясняет Ватсону ход своих рассуждений: «Отпечаток заднего колеса всегда глубже, потому что на него приходится б о льшая тяжесть. Вот, видите? В нескольких местах он совпал с менее ясным отпечатком переднего и уничтожил его. Нет, велосипедист, несомненно, ехал от школы».

Я не уверен, что понимаю эти рассуждения. Безусловно, заднее колесо скрыло след переднего, но в каком направлении ехал велосипедист? Создатель Холмса сэр Артур Конан Дойл упустил одну важную деталь. Определить направление движения велосипеда по отпечатку шины действительно возможно.

Ответ

В каком направлении – слева направо или справа налево – ехал велосипедист, оставивший эти следы?

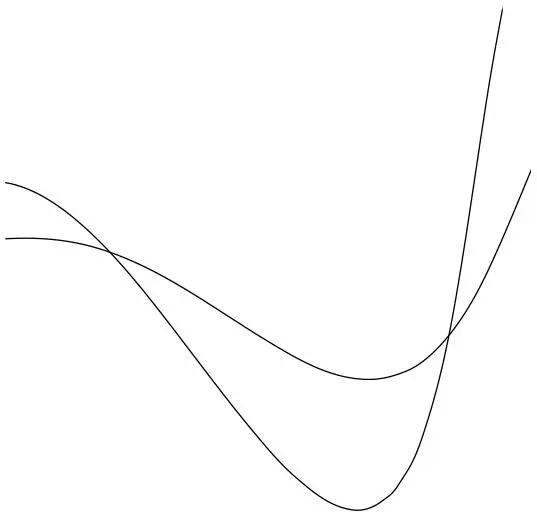
Холмс был прав в том, что сначала необходимо определить, какой след оставлен каким колесом. Но это можно сделать, не зная глубины отпечатка велосипедных шин.

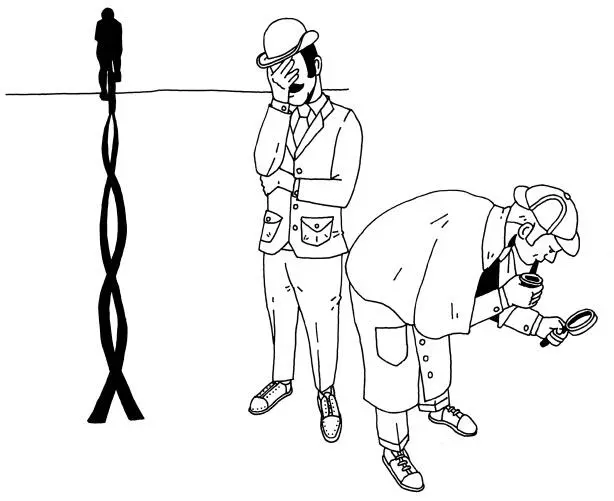
А вот еще одна загадка о движении велосипеда. Ответ вы можете понять интуитивно. Одно изображение покажется вам правильным, а другое нет. Но удастся ли вам объяснить почему?

Ответ

Фотограф снимает движущийся велосипед. Велосипед едет по горизонтальной дороге либо слева направо, либо справа налево – направление не имеет значения. Колесо – это белый диск, на котором изображены два пятиугольника.

Какое из двух изображений на рисунке – фотография, сделанная фотографом?

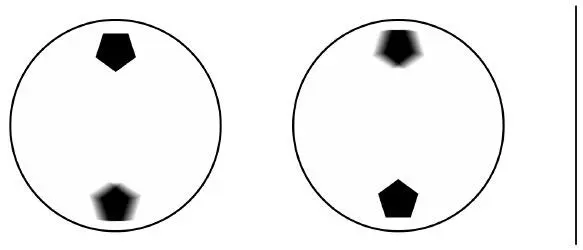
Соль этой головоломки в том, что предсказать движение катящейся окружности сложнее, чем кажется на первый взгляд.

Следующая задача взята из теста на проверку общих способностей (SAT), который в 1982 году прошли 300 тысяч американцев. Только три ученика решили ее правильно. А вы сможете?

Ответ

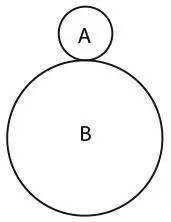
Радиус окружности A равен 1/3 радиуса окружности B. A совершает один оборот вокруг B и возвращается в исходную точку. Сколько раз окружность A обернется вокруг своего центра за это время?

а) ;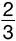

б) 3;

в) 6;

г) ;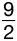

д) 9.

А теперь обратимся к головоломке, которая заставит вас размышлять совершенно иначе.

Ответ

На столе лежат восемь квадратных листов бумаги одинакового размера. Их края образуют следующий рисунок, причем только лист под номером 1 виден полностью.

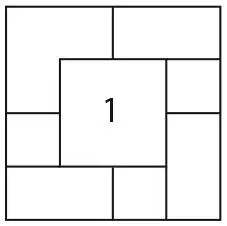
Можете ли вы пронумеровать все остальные листы с учетом того, что 2 означает второй уровень, 3 – третий и т. д.?

Впервые о задаче с чистыми листами бумаги я узнал из блестящей книги Кобона Фуджимуры The Tokyo Puzzles («Токийские головоломки»).

В 1930–1970-х годах Фуджимура был королем головоломок в Японии. Он написал и опубликовал много книг, в том числе несколько бестселлеров, а в 1950-х даже организовал собственную еженедельную телепрограмму о головоломках. Популярность Фуджимуры явилась предвестником современного бума японских головоломок, вершиной которого стал международный успех судоку в 2000-х годах (об этом я расскажу подробнее чуть дальше в этой главе).

Японцы склонны более игриво относиться к числам, чем жители стран Запада, – во всяком случае, так мне показалось во время двух визитов в Японию. Японские школьники рассказывают таблицу умножения с такой же радостной непринужденностью, как и детские стишки. В прошлом популярным развлечением в этой стране были игры с числами на билетах метро. Кроме того, в Японии ментальную арифметику [18]превратили в зрелищное состязание. Овладение навыками вычислений на счетах – популярное внеклассное занятие, а для лучших мастеров в этом деле проводятся турниры. В 2012 году я побывал на национальном чемпионате по счету на счетах, кульминацией которого стала игра, в ходе которой участники состязания должны были на воображаемых счетах сложить 15 чисел, демонстрируемых им менее чем за две секунды. Это было напряженное и захватывающее соревнование!