Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

4. Джон и Пол совершают последний переход, потратив на это еще 2 минуты.

Суммарное время составляет 2 + 1 + 10 + 2 + 2 = 17 минут.

Эта головоломка превосходна, поскольку в ней действие, которое на первый взгляд кажется нерациональным (уменьшить участие Джона), на самом деле именно то, что нужно совершить. Такое решение вызывает восхищение.

Чтобы понять, почему двум друзьям, передвигающимся медленнее всех, лучше всего идти вместе, представьте, что Джон переходит через мост за 1 минуту, Пол – за 2 минуты, но Джорджу понадобится 24 часа, а Ринго – 24 часа и 1 минута. Теперь стало гораздо очевиднее, почему Джордж и Ринго должны вместе перейти через мост с фонарем, ведь для этого понадобится только один переход продолжительностью 24 часа.

К тексту

Два сына – одновременно и дяди, и племянники друг другу. Для простой головоломки ее условия на удивление запутанны. Назовем двух мужчин Альбертом и Бернардом, а их сыновей – Стивом и Тревором. Ниже изображено генеалогическое дерево.

Бернард и Стив – единокровные братья, поскольку у них одна мать. Следовательно, сын Бернарда Тревор – племянник Стива.

Аналогично Альберт и Тревор – единокровные братья, а значит, Стив – племянник Тревора.

Сложные семейные связи становятся еще запутаннее, если принять во внимание, что мать Бернарда замужем за Альбертом, – следовательно, мачеха матери Бернарда является матерью Альберта. Это делает мать Альберта неродной бабушкой Бернарда. Таким образом, Бернард состоит в браке со своей неродной бабушкой.

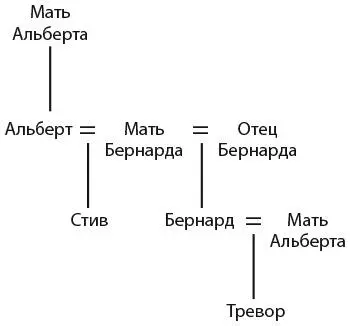
К тексту

На званом ужине присутствует только один гость.

На представленной ниже схеме показаны родственные связи в этой странной семье. Отец губернатора – мистер C, а значит, этот гость – шурин отца губернатора. Таким же образом каждое из описаний гостей ведет нас от губернатора к гостю: через брата губернатора (мистера E), через его тестя (мистера B) и через шурина (мистера D).

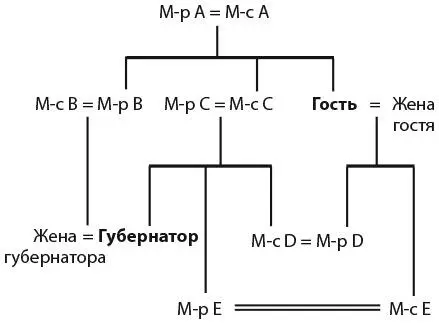
К тексту

Мы ищем такое сочетание правдивого и лживого утверждений, которое не ведет к противоречию.

Предположим, Берта говорит правду. Из этого следует, что Грета лжет, а значит, Роза должна говорить правду. Но если она говорит правду, то Берта и Грета лгут, что является противоречием. Следовательно, Берта не говорит правду.

Если Берта лжет, то Грета говорит правду, а это значит, что лжет Роза. Если же она лжет, то по меньшей мере одна из двух девушек (Берта или Грета) говорит правду, а это верное утверждение. Таким образом, сочетание утверждений, при которых Берта и Роза лгут, а Грета говорит правду, является логически непротиворечивым. Это и есть решение задачи.

К тексту

В условии задачи сказано, что ближайший сосед кондуктора зарабатывает втрое больше него. Значит, ближайшим соседом кондуктора не может быть господин Джонс, поскольку его заработная плата не делится на три. Однако ближайшим соседом кондуктора не может быть и господин Робинсон, потому что кондуктор живет между Лидсом и Шеффилдом, а господин Робинсон – в Лидсе. Следовательно, ближайшим соседом и обитателем города «между Лидсом и Шеффилдом» должен быть господин Смит. Мы можем поставить галочку в правой верхней ячейке правой таблицы, как показано ниже, и сделать вывод, что господин Джонс живет в Шеффилде, так как это единственный оставшийся вариант.

Тезка кондуктора живет в Шеффилде, а нам известно, что мистер Джонс живет в Шеффилде. Стало быть, кондуктором должен быть Джонс. Как показано на рисунке ниже слева, мы можем отметить галочкой ячейку «Джонс – кондуктор», а также проставить крестики в других ячейках в той же строке и том же столбце, потому что у Джонса нет другой профессии, а остальные не являются кондукторами.

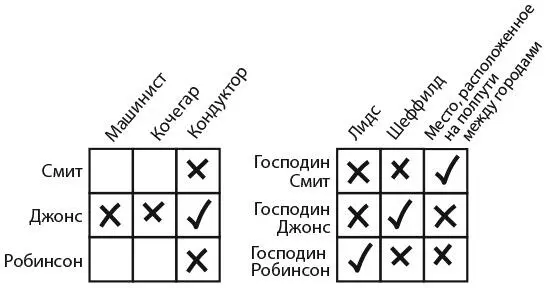
Подсказка о том, что Смит может выиграть у кочегара в бильярд, позволяет сделать вывод, что Смит не кочегар. (Кочегаром должен быть Робинсон.) Таким образом, мы ставим крестик в ячейке «Смит – Кочегар». Мы уже знаем, что Смит не кондуктор. Таким образом, методом исключения приходим к выводу, что Смит – машинист.

К тексту

Определить, кто из девочек ходил в кино, можно, перебрав всех по одной, каждый раз исходя из того, что данная девочка была в кинотеатре, и подсчитывая, сколько девочек лгут.

Предположим, в кино ходила Джоан Джаггинс. Ее утверждение о том, что это была Джоан Твигг, не соответствует действительности, как и утверждение Герти Гасс. Однако Бесси и Салли, должно быть, говорят правду. Когда мы отметим это в таблице, нам легче будет выявить закономерность. В первой строке представленной ниже таблицы отображена правдивость или ложность утверждений в случае, если Джоан Джаггинс была в кино, во второй строке – если в кино была Герти Гасс и т. д. В последнем столбце отображено общее количество ложных утверждений. Таким образом, если П – правда, а Л – ложь, первая строка начинается с последовательности Л, Л, П, П, а вся таблица выглядит следующим образом:

Если по меньшей мере семь утверждений не соответствуют действительности, значит, тайным киноманом должна быть Дороти Смит.

К тексту

Итак, у нас есть пять мужчин: Дженкинс, Томкинс, Перкинс, Уоткинс и Симкинс, для простоты – Д, Т, П, У и С. И есть пять женщин, которые являются матерями и женами конкретных мужчин, причем одна и та же женщина не может быть одновременно женой и матерью одного мужчины – любовь в Кинсдейле, конечно, странная, но не настолько. Давайте определим этих женщин по их родственным связям и обозначим эти связи строчными буквами: д – мать Д, т – мать Т и т. д.

Далее нарисуем таблицу, верхняя строка которой соответствует мужчинам, а нижняя – их женам, то есть сначала вторая строка пуста. Если Томкинс – пасынок Дженкинса, значит, миссис Дженкинс – мать Томкинса, поэтому можно вписать букву т под Д.

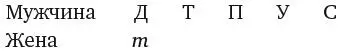
Нам также известно, что Томкинс – отчим Перкинса, а это значит, что миссис Томкинс – мать Перкинса. Следовательно, под Т пишем п.

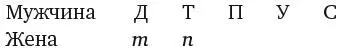
По условиям задачи, мать Перкинса – подруга миссис Уоткинс. Следовательно, мы знаем, что миссис Уоткинс не мать Дженкинса. Поскольку миссис Уоткинс не может быть матерью Уоткинса, методом исключения мы приходим к выводу, что она должна быть матерью Симкинса.