Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Единственное пятизначное автобиографическое число – 21 200.

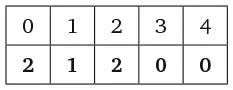
В этом числе две цифры 0, одна цифра 1, две цифры 2, нет цифр 3 и 4.

Поняли принцип? Значит, вы готовы решить следующую задачу.

Ответ

Найдите единственное десятизначное автобиографическое число.

Это число будет расположено во второй строке представленной ниже таблицы. Каждая его цифра должна означать частоту встречаемости верхней цифры во второй строке.

Число, в котором есть все десять цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 и 0 (например, 1 234 567 890), называется панцифровым. (Крайняя цифра слева панцифрового числа должна отличаться от нуля.)

Ответ

Сколько существует десятизначных панцифровых чисел?

Интересный факт: все десятизначные панцифровые числа делятся на 3. Мы можем продемонстрировать это, применив признак делимости на 3, который вы, возможно, помните еще со школьных времен. Число делится на 3, если сумма его цифр делится на 3.

Десятизначное панцифровое число должно содержать каждую цифру только один раз. Таким образом, в результате сложения мы получим 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 = 45, а это число делится на 3. Следовательно, все панцифровые числа делятся на 3. Изумительно!

А вот менее известные признаки делимости:

Признак делимости на 4: число делится на 4, если две его последние цифры составляют число, которое делится на 4.

Признак делимости на 8: число делится на 8, если три его последние цифры составляют число, которое делится на 8.

Возможно, вы захотите подумать над тем, почему эти два признака верны. А может, и нет. Как бы там ни было, они пригодятся вам в следующей головоломке.

Ответ

Найдите десятизначное панцифровое число abcdefghij, в котором:

• a делится на 1;

• ab делится на 2;

• abc делится на 3;

• abcd делится на 4;

• abcde делится на 5;

• abcdef делится на 6;

• abcdefg делится на 7;

• abcdefgh делится на 8;

• abcdefghi делится на 9;

• abcdefghij делится на 10.

Эта задача поразительно изящная, поскольку ее условие подразумевает наличие единственного решения. Вам понадобится калькулятор, что, впрочем, не испортит удовольствия при поиске ответа.

Придумайте трехзначное число, первая и последняя цифры которого должны отличаться минимум на 2. Пусть это будет, например, число 258.

Запишите его в обратном порядке и вычислите разность между двумя данными числами. В моем примере это 852–258 = 594.

Сложите полученный результат с его обращенным числом: 594 + 495.

Ответ – 1089.

Теперь попробуйте сделать то же самое с другим числом: запишите его в обратном порядке, вычислите разность, сложите полученный результат с его обращенным числом и…

Вы уже догадались! Ответ – 1089.

Каким бы ни было исходное трехзначное число, вы всегда будете получать один и тот же ответ – 1089. Этот факт неизменно производит большое впечатление на всех, кто сталкивается с ним впервые.

Итак, в арифметическом смысле 1089 – особенное число. И на то есть еще одна причина помимо вышеописанной.

Ответ

При умножении числа 1089 на 9 получится его обращенное число: 1089 × 9 = 9801.

Найдите четырехзначное число, произведение которого на 4 представляет собой то же число, но записанное в обратном порядке. Другими словами, найдите такое число abcd, при условии, что abcd × 4 = dcba.

Число 102 564 также очень интересно меняется в случае умножения на 4:

102 564 × 4 = 410 256.

Вы заметили закономерность? Последняя цифра числа 102 56 4становится первой цифрой числа 410 256, тогда как все остальные цифры не меняются. Иначе говоря, при умножении 102 546 на 4 получается число, представляющее собой тот же набор цифр, в котором крайняя цифра справа исходного числа перемещается в крайнюю левую позицию полученного числа.

Такая же трансформация происходит и в следующем примере:

142 85 7× 5 = 714 285.

Крайняя правая цифра первого числа (в данном случае 7) становится первой цифрой произведения, а остальные цифры остаются теми же.

Ответ

Найдите такое число N, чтобы результат его умножения на 2 состоял в точности из тех же цифр и в том же порядке, что и число N, за исключением его крайней правой цифры, которая является первой цифрой ответа. Другими словами, при умножении числа N на 2 с ним происходит то же самое, что и с произведением числа 102 564 на 4 и числа 142 857 на 5.

На одной научной конференции выдающийся британский физик Фримен Дайсон услышал в кафе обсуждение этой задачи. «О, да это же совсем просто! – вмешался он в разговор. – Но, конечно же, наименьшее такое число содержит 18 цифр».

Как отмечалось в New York Times, коллеги Дайсона были поражены. Никто понятия не имел, как ему удалось получить результат: «Либо Фримен знал ответ, либо, что еще более поразительно, смог вывести его в уме за пару секунд».

Как бы там ни было, Дайсон оказался прав, а для того чтобы найти решение, необходимо знать математику на уровне ученика начальной школы.

Мы приближаемся к концу книги, а числа становятся все больше. Вообще говоря, они настолько велики, что не уместятся на одной странице.

Ответ

Представленные ниже девять чисел – последние четыре цифры чисел 31 9, 32 9, 33 9, 34 9, 35 9, 36 9, 37 9, 38 9, 39 9, перечисленные в случайном порядке. Расположите их в порядке возрастания.

…2848

…5077

…1953

…6464

…8759

…8832

…0671

…1875

…8416

Следующее число относится к числу 39 9свысока за недостаточное прилежание.

Ответ

[37]

Определите приближенное значение 2 64.

И последнее число считает ничтожным даже число 2 64.

Ответ

Сколько нолей в конце числа 100?!

Как уже было сказано в этой книге, 100! означает, что результат получен путем умножения числа 100 на все целые числа меньше 100. Следовательно, число 100! равно 100 × 99 × 98 × 97 × 96 × … × 3 × 2 × 1. Вам не обязательно вычислять ответ – он состоит из 158 цифр. Лучше используйте свое глубокое понимание математики и определите, что означают ноли в конце числа.

Ответ

1. г) М.