Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Ответ

– =

×

÷ =

=

+ = .

Ответ

× = .

× = .

Ответ

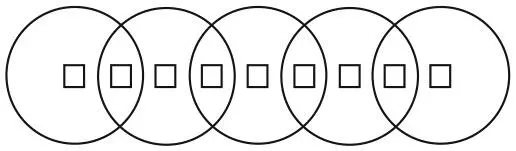
В этой головоломке содержатся три задачи. Заполните пустые ячейки так, чтобы сумма цифр в каждом круге равнялась 11. Решите эту задачу еще раз, чтобы сумма чисел в каждом круге составляла 13, и еще раз, чтобы сумма была равна 14.

Книга Томаса Дилворта The Schoolmaster’s Assistant, Being a Compendium of Arithmetic both Practical and Theoretical («В помощь учителю: краткое руководство по практической и теоретической арифметике») вышла в 1743 году и стала чрезвычайно популярным учебником по математике в Великобритании и США. В ней есть такая задача:

Джек говорит своему брату Гарри: «Я могу связать четыре тройки знаками математических операций таким образом, что они образуют число 34. Сможешь ли ты сделать то же самое?»

Ответ такой: 33 + 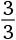= 34.

В книге Дилворта впервые появились головоломки, в которых требовалось связать четыре одинаковые цифры знаками математических операций и получить определенное число. В трех предыдущих задачах из этой главы заданы математические операции, а тот, кто решает задачу, должен разместить числа между соответствующими знаками. В представленных ниже головоломках даются числа, между которыми нужно расставить знаки математических операций. Самый распространенный вариант головоломок такого рода – это задача о четырех четверках, впервые упомянутая спустя столетие после Дилворта. В 1881 году автор под псевдонимом Cupidus Scientiae (Жаждущий науки) написал в британском журнале Knowledge: an Illustrated Magazine of Science следующее: «Возможно, некоторым читателям это покажется столь же новым, как и мне, когда на днях мне впервые продемонстрировали, что все числа до двадцати включительно (и даже больше), кроме разве что числа 19, можно представить в виде четырех четверок, воспользовавшись любыми необходимыми математическими знаками за исключением знаков возведения в квадрат и куб».

«Четыре четверки» – невероятно интересная головоломка, забавная, простая и увлекательная. Поистине удивительно, сколько чисел можно составить с помощью цифр 4, 4, 4 и 4 – не больше и не меньше. Однако нам следует внести ясность в утверждение Cupidus Scientiae о том, какие для этого существуют возможности и какие знаки разрешается использовать.

Ответ

1. С помощью четырех четверок составьте все числа от 0 до 9. Разрешается применять только основные математические операции, такие как сложение, вычитание, умножение, деление, и скобки. Помните: для выражения каждого числа необходимо использовать все четыре четверки.

2. С помощью четырех четверок составьте все числа от 10 до 20. В дополнение к основным знакам математических операций можно использовать квадратный корень, а также запятую для обозначения нецелых чисел, например 0,4. Кроме того, можно объединять цифры в группы – скажем, 44, или 444, или даже 4,4.

3. После того как немного разогреетесь, проделайте то же самое с числами от 21 до 50. Разрешается использовать возведение в степень, то есть 4 4, а также знак факториала «!», как в выражении 4!. (Для того чтобы получить факториал числа, необходимо умножить его на каждое меньшее число, например: 4! = 4 × 3 × 2 × 1 = 24.)

Я помогу вам начать решать эту задачу. Вот как можно получить 0 из четырех четверок:

4 – 4 + 4–4 = 0

Очень просто. А вот как можно получить 1:

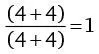
Насколько далеко мы можем зайти после числа 50? Очень далеко. С помощью перечисленных выше математических операций мы можем составить из четырех четверок все числа до 100, за исключением чисел 73, 77, 87 и 99, хотя даже их можно получить благодаря находчивому применению дополнительных математических символов. Например:

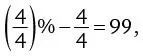
поскольку четыре четверти составляют 100 процентов.

В издании книги «Математические эссе и развлечения» 1911 года Уолтер Роуз Болл о «четырех четверках» писал: «Никогда не встречал этой занимательной задачи в печатных изданиях, но, похоже, она старая и широко известная».

Роуз Болл утверждал, что с помощью четырех четверок можно составить все числа до 170. До выхода издания 1917 года Роуз Болл был поглощен работой над этой головоломкой. «Если мы допустим использование целых показателей степени и применение факториалов, – писал он, – то сможем добраться до числа 877». Далее он отметил: «С помощью четырех единиц мы можем получить число 34, четырех двоек – число 36, четырех троек – число 46, четырех пятерок – число 36, четырех шестерок – 30, четырех семерок – 25, четырех восьмерок – 36, четырех девяток – 130». Интересно, что с помощью четырех четверок можно зайти дальше всего.

Удалось ли кому-либо сделать это? Да! На протяжении следующего десятилетия математик и физик Поль Дирак (с ним мы уже встречались в конце предыдущей главы) решил задачу о четырех четверках для всех чисел до бесконечности. Его решение касалось задачи с четырьмя двойками – в то время она была весьма популярна в Кембридже, – но оно верно и для задачи о четырех четверках.

Если разрешено применять логарифмы, то любое число n можно представить в следующем виде: 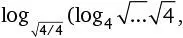где n – количество квадратных корней в выражении. (Не огорчайтесь, если не понимаете логарифмы; вам нужно всего лишь по достоинству оценить поразительную лаконичность и масштабируемость решения.) Дираку нравились математические головоломки, и, по всей вероятности, он был в восторге от того, что ему удалось обобщить знаменитую задачу с помощью столь изобретательной формулы. «Он сделал эту задачу бессмысленной», – писал Грэм Фармело в биографии Поля Дирака The Strangest Man («Самый странный человек»).