Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Лишь одно утверждение истинно.

Лишь два утверждения истинны.

Все утверждения истинны.

Варианты ответов:а) 0; б) 1; в) 2; г) 3; д) 4.

Ответ

2. Какая из фигур не может образоваться при наложении двух одинаковых квадратов?

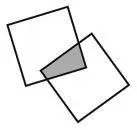
Варианты ответов:а) равносторонний треугольник; б) квадрат; в) дельтоид [33]; г) семиугольник; д) правильный восьмиугольник.

Ответ

3. Только одно из следующих уравнений верно? Какое именно?

Варианты ответов:

а) 44 2 + 77 2 = 4477;

б) 55 2 + 66 2 = 5566;

в) 66 2 + 55 2 = 6655;

г) 88 2 + 33 2 = 8833;

д) 99 2 + 22 2 = 9922.

Ответ

4. Сколько существует способов расположения в один ряд пяти переключателей во включенном или выключенном положении таким образом, чтобы никаких два соседних переключателя не находились в выключенном положении?

Варианты ответов:а) 5; б) 10; в) 11; г) 13; д) 15.

Ответ

5. В приведенной ниже записи сложения буквами обозначены разные цифры; буквой S обозначена цифра 3. Чему равно значение Y × O?

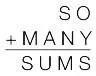
Варианты ответов:а) 0; б) 2; в) 36; г) 40; д) 42.

Ответ

6. Электронные часы показывают часы, минуты и секунды. Сколько раз за каждые 24 часа все шесть цифр меняются одновременно?

Варианты ответов:а) 0; б) 1; в) 2; г) 3; д) 4.

Ответ

7. Один из следующих кубов – наименьший куб, который может быть записан в виде суммы трех положительных кубов. Что это за число?

Варианты ответов:а) 27; б) 64; в) 125; г) 216; д) 512.

Ответ

8. В последовательности чисел каждый четвертый член представляет собой сумму трех предыдущих членов. Первые три члена – это −3, 0, 2. Какой по счету номер первого члена этой последовательности, превышающего значение 100?

Варианты ответов:а) 11-й; б) 12-й; в) 13-й; г) 14-й; д) 15-й.

Ответ

9. Страницы книги пронумерованы: 1, 2, 3… Для того чтобы пронумеровать все страницы, понадобится 852 цифры. Назовите номер последней страницы.

Варианты ответов:а) 215; б) 314; в) 320; г) 329; д) 422.

Ответ

10. На рисунке изображен единичный куб (то есть куб, длина ребра которого равна 1), окрашенный в голубой цвет. Предположим, что к каждой из его шести граней приклеены единичные кубы голубого цвета, образующие трехмерный крест. Сколько единичных кубов желтого цвета понадобится для того, чтобы оклеить все свободные грани этого креста?

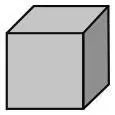
Варианты ответов:а) 6; б) 18; в) 24; г) 30; д) 36.

Ответ

Сборник математических задач не был бы полным без числовых головоломок. Речь идет не о головоломках, основанных на числах (в предыдущих главах мы видели их предостаточно), а о тех логических задачах, которые без всякого стеснения превозносят числа и раскрываемые ими закономерности. В их условия не нужно вводить никакие предметы и приемы, чтобы повысить заинтересованность в их решении. Процесс приносит удовольствие уже сам по себе. Но даже несмотря на такую особенность, головоломки с числами бывают невероятно забавными. Развлечением может стать даже такое простое арифметическое действие, как сложение.

Можете ли вы просуммировать числа от 1 до 100?

В XVIII столетии великий математик Карл Гаусс мгновенно решил эту старую задачку, еще когда носил короткие штанишки. Во всяком случае, так гласит легенда. Учитель ожидал, что мальчик станет складывать числа по одному, но гениальный ученик нашел закономерность.

Чтобы найти сумму чисел

1 + 2 + 3 + 4 + … + 97 + 98 + 99 + 100,

можно просуммировать пары крайних чисел:

(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + … + (50 + 51).

Сумма этих пар чисел всегда одна и та же:

101 + 101 + 101 + 101 + … + 101.

Следовательно, общая сумма равна 50 раз по 101, или 50 × 101 = 5050.

Умница Карл! Эту историю обычно рассказывают так, будто Гаусс был первым, у кого возникла такая идея. Однако эта задача была включена в сборник Алкуина «Задачи для развития молодого ума» еще тысячу лет назад.

У лестницы 100 ступеней. На первой сидит один голубь, на второй – два, на третьей – три и так далее до сотой ступени. Сколько всего голубей сидит на лестнице?

Хотя задача сформулирована иначе, арифметика в ней та же – сложение чисел от 1 до 100. Решение Алкуина также подразумевало сложение пар, но других. Он находил сумму первой и последней ступеней лестницы, получив 1 + 99 = 100, затем второй и предпоследней и т. д.

Следовательно, сумма равна (1 + 99) + (2 + 98) + (3 + 97) + … + (49 + 51) плюс 50 с пятидесятой ступени и 100 с сотой ступени, что равно:

(49 ×100) + 50 + 100 = 4900 + 150 = 5050.

Хотя решение Алкуина более громоздкое, чем Гаусса, оно легче, поскольку умножить на 100 проще, чем на 101. Если вы, подобно Алкуину, используете римские цифры, делайте так, как он.

Соль этих двух головоломок в том, что, если вам предлагают вычислить сумму большой группы чисел, не воспринимайте задание буквально, а попытайтесь найти закономерность.

Ниже представлены три замечательные головоломки со счетом. При их решении вы сможете применить этот принцип на практике.

Какая из двух сумм больше?

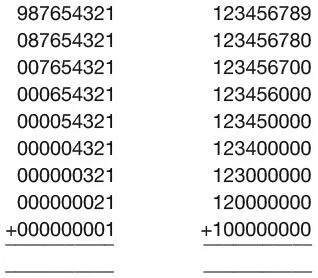
Ответ

Ниже в порядке возрастания приведены 24 четырехзначных числа, состоящие из цифр 1, 2, 3 и 4. Вычислите сумму этих чисел.

1234 1423 2314 3124 3412 4213

1243 1432 2341 3142 3421 4231

1324 2134 2413 3214 4123 4312

Ответ

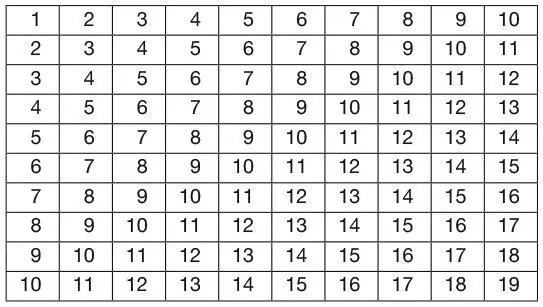
А теперь запишем числа в таблицу. Вы знаете, что делать. Чему равна их сумма?

Следующие три головоломки – настоящая поэзия в математике. В каждой есть схема с девятью пустыми ячейками, в которых должны находиться цифры от 1 до 9. Восхитительно видеть, как простейшие числовые элементы – значащие цифры – изящно располагаются в пустых ячейках.

Существует 24 192 способа разместить девять цифр в каждой из этих схем. Если проверять новую комбинацию каждую секунду, то, чтобы перебрать все варианты, понадобилось бы больше двух недель. Так что попытайтесь найти способ сократить количество возможных комбинаций.