Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Далее мы с вами сыграем в солитер с монетами. В игре действуют обычные правила: любая монета может перешагнуть через соседнюю и занять место с другой стороны, после чего монета, через которую перешагнули, удаляется с поля. Как и в шашках, при желании можно ходить через несколько монет за один шаг, если монета занимает позицию, в которой возможен следующий шаг.

Ответ

Расположите десять монет треугольником, как показано на рисунке. Одну монету уберите. Теперь, перешагивая через другие монеты, уменьшите треугольник до одной монеты.

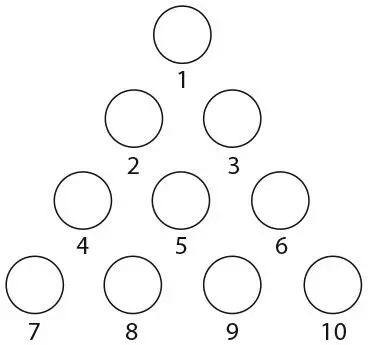
Как и предыдущие головоломки с монетами, эта тоже всецело поглотит ваше внимание, пока вы ее не решите. Но прежде чем вы начнете, рекомендую разложить монеты на листе бумаги, на котором отмечены 10 точек, чтобы монеты не смещались со своих мест.

Поиграв немного, вы можете обнаружить следующее решение за шесть ходов после удаления монеты с позиции 2:

1. Монета на позиции 7 перемещается на позицию 2 (монета на позиции 4 удаляется).

2. Монета 9 перемещается на 7 (8 удаляется).

3. 1 перемещается на 4 (2 удаляется).

4. 7 перемещается на 2 (4 удаляется).

5. 6 перемещается на 4, затем на 1, а затем на 6 (5, 2 и 3 удаляются).

6. 10 перемещается на 3 (6 удаляется).

Но мы можем решить эту головоломку и за пять ходов. Попробуйте найти такое решение.

В эту главу я включил полдюжины задач с монетами (почти полглавы), поскольку монеты – самый универсальный предмет из всех используемых в головоломках. Существует много способов применения монет: их можно передвигать, не отрывая от поверхности, укладывать стопками, использовать в качестве геометрических точек или колышков для «Солитера». Кроме того, у монет две различающиеся стороны, что положено в основу следующей головоломки (или фокуса).

Ответ

Представьте, что вы фокусник и у вас завязаны глаза. Вы предлагаете одному из зрителей положить десять монет на стоящий перед вами стол и сообщить вам, сколько монет перевернуты орлом вверх.

Вы не видите монеты, а значит, не можете определить, какой стороной они расположены вверх.

Как вам разделить монеты на две группы таким образом, чтобы в обеих группах было одинаковое количество орлов?

Когда я впервые увидел этот фокус, я был впечатлен, но его решение поразило меня гораздо больше.

Попытайтесь сначала решить задачу с открытыми глазами. Возьмите десять монет и разложите их на столе так, чтобы было видно, скажем, три орла. Попробуйте разделить монеты на две группы, чтобы в обеих оказалось одинаковое количество орлов. Поскольку три орла не делятся на два без остатка, вам придется перевернуть несколько монет. Ключ к решению головоломки – понять, сколько монет нужно перевернуть, а затем придумать, как проделать то же самое с завязанными глазами.

Головоломка с монетами в темноте похожа на фокус, так как в ходе ее решения неожиданно наступает приятное озарение. Вообще-то многие головоломки напоминают трюки фокусника, и не только потому, что их решение – это своего рода откровение, но и потому, что зачастую они основаны на неявном введении в заблуждение.

Я включил следующую задачу в эту главу, потому что в ней тоже используются монеты, а решение поразительно. Конечно, я не рассчитываю на то, что вы и правда станете раскладывать на столе сотню монет, но, если вам не удастся найти ответ, все же настоятельно рекомендую прочитать его, хотя бы из любопытства. Впервые эта задача была задана в 1996 году на Международной олимпиаде по информатике – конкурсе для школьников, который изначально был ориентирован на очень умных подростков – компьютерных гиков. Это замечательная задача.

Ответ

На столе выложены в ряд сто монет. Пенни и Боб играют в игру, их задача – собрать максимальную сумму денег, поочередно забирая монеты со стола. Игроки могут брать только монеты, находящиеся в конце ряда. Монеты имеют разное достоинство: 1 пенни, 2 пенни, 1 фунт и т. д.

Первой ходит Пенни. Она берет монету с одного конца и кладет ее в карман. Боб забирает монету с другого конца ряда и тоже кладет себе в карман. Так они по очереди берут монеты до тех пор, пока на столе ничего не остается. За каждый ход игроки могут брать монету с любого конца.

Удастся ли вам доказать, что Пенни при любых обстоятельствах может собрать не меньшую сумму денег, чем Боб?

Подсказка: пронумеруйте монеты от 1 до 100.

Ладно, хватит уже игр с монетами! Давайте перейдем к головоломкам со спичками – этот предмет издавна занимает второе место по популярности в головоломках. Однако сначала предлагаю разобрать головоломку, в которой фигурируют и монета, и спички. Считайте ее эквивалентом редкого дуэта двух старых эстрадных певцов в области занимательной математики.

Ответ

Два перевернутых стакана стоят так, как показано на рисунке. Между ними находится спичка; под левым стаканом лежит монета. Можете ли вы достать монету из-под стакана так, чтобы спичка не упала?

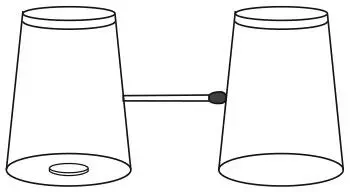
Спички были изобретены в XIX веке, и на протяжении сотни лет задачи со спичками были, пожалуй, самыми распространенными головоломками, которые решали представители разных поколений. Сейчас спички используются не так широко, как раньше, поскольку меньше людей курят, а у курящих, как правило, есть зажигалки. Приемлемой заменой спичкам могут стать зубочистки, карандаши или ватные палочки.

Генри Дьюдени называет следующую задачу «небольшой головоломкой для юных читателей».

Ответ

На рисунке изображено 16 спичек, которые образуют равносторонние треугольники.

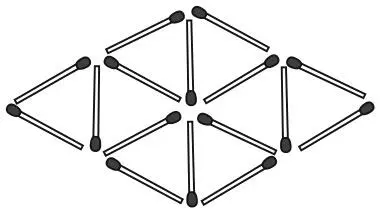
Уберите четыре спички так, чтобы осталось ровно четыре равносторонних треугольника и не было открытых концов и лишних спичек.

Ответ

Разложите 12 спичек в форме шестиугольника, состоящего из шести равносторонних треугольников.

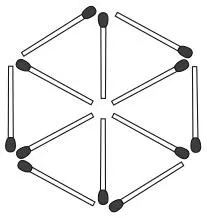
Эта головоломка решается за четыре шага.

1. Передвиньте две спички на другие места так, чтобы осталось пять равносторонних треугольников.