Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

На рисунке видно, что на кубе изображено шесть букв: I, K, M, O, U и P. Поскольку у куба шесть граней, на нем могут быть написаны только эти буквы. На первой картинке грани с буквами I и M имеют общее ребро с гранью буквы K. На второй – общее ребро с гранью буквы K у O и U. Только у четырех граней может быть общее ребро с гранью буквы K. Если расположить куб так, чтобы грань с буквой K была сверху (как на первой картинке), то грань с буквой I будет смежной грани с буквой M по часовой стрелке. На основании второй картинки мы можем сделать вывод, что, когда грань с буквой K находится сверху, грань с буквой O смежна грани с буквой U по направлению движения часовой стрелки, а значит, грани куба расположены по часовой стрелке в следующем порядке: M-I-U-O. Таким образом, на грани, противоположной грани с буквой U, находится буква M.

К тексту

2. г) теннисного корта.

После того как Пиноккио солжет девять раз, длина его носа составит 2 9× 5 см = 512 × 5 см = 25,6 м, что примерно равно длине теннисного корта, которая равна 23,8 метра. Однако, согласно отчету Центра междисциплинарных наук при Университете Лестера, эта длина намного меньше возможной максимальной длины носа Пиноккио. Расчеты специалистов центра показывают, что если деревянная голова Пиноккио весит 4,18 килограмма, а нос – 6 граммов, первоначальная длина которого составляет один дюйм (2,54 см), то нос сломается только после 13 случаев вранья, когда он вырастет до 208 метров.

К тексту

3. в) eighteen (18).

В слове eighteen (18) восемь букв, а число 18 не кратно 8.

К тексту

4. г) Эми – крайняя слева.

Эми находится по левую сторону и от Бена, и от Криса. Следовательно, эти трое стоят в таком порядке: Эми, Бен, Крис или Эми, Крис, Бен. Это все, что нам известно, поэтому утверждение «г» однозначно верно. Ни одно из оставшихся утверждений не должно быть истинным, хотя утверждение «б» может быть истинным.

К тексту

5. E.

Эту задачу можно решить методом проб и ошибок. Можно также доказать следующее правило: чтобы нарисовать изображение, не отрывая карандаша от бумаги и не проводя карандашом по линии повторно, оно должно содержать не более двух точек, в которых сходится нечетное количество линий. Этому условию удовлетворяет только ответ E, поскольку на изображении вообще нет точек, в которых сходится нечетное количество линий, тогда как на других рисунках таких точек больше двух [38].

К тексту

6. б) 2.

Надеюсь, вы знаете хотя бы таблицу умножения на семь! В таком случае для вас не станет неожиданностью тот факт, что 35 делится на 7, а значит, и 350 000 делится на 7. На 7 делится также 49, и 4900. Поскольку 354 972 = 350 000 + 4900 + 72, остается только найти остаток от деления 72 на 7. Так как 7 × 10 = 70, остаток равен 2.

К тексту

7. в) 4.

В семье должно быть по меньшей мере два мальчика, поскольку если бы мальчик был только один, у него не было бы брата, что противоречит условиям задачи. Аналогично, в семье должно быть по меньшей мере две девочки, а значит, в семье минимум четверо детей.

К тексту

8. д) 9.

Просто выполните это забавное умножение на любом клочке бумаги – и задача решена.

К тексту

9. а) 3.

Надеюсь, на вашем листе бумаги еще осталось место. Впишите в пустые клетки пирамиды (начиная сверху и слева направо) буквы p, q, r ; в правую крайнюю клетку в четвертом ряду s и в пятом ряду между клетками с числом 9 и буквой х – t. Вот необходимые вычисления:

p = 105 – 47 = 58;

q = p – 31 = 58–31 = 27;

r = 47 – q = 47–27 = 20;

s = r – 13 = 20–13 = 7;

t = 13 – 9 = 4;

х = s – t = 7–4 = 3.

К тексту

10. а) 2.

С моей стороны было бы неучтиво не включить задачу на деление в столбик, в результате чего получим 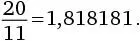поэтому десятичная дробь содержит только две разные цифры.

К тексту

Решить задачу с девятью переправами можно следующим образом. (Надо отметить, что, по условиям задачи, мужчин нельзя назвать джентльменами еще и потому, что женщины вынуждены грести по меньшей мере во время шести переправ – а может, и во время всех.) В целом стратегия такова: нужно взять первую пару, а затем вторую и третью и т. д. при условии, что братья всегда сходят на берег раньше сестер.

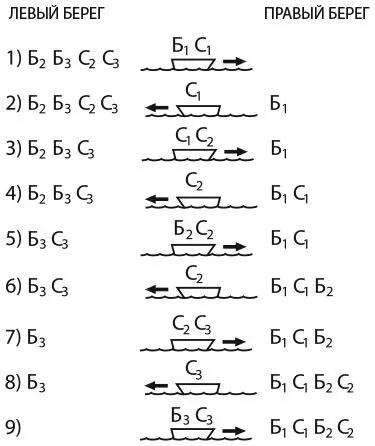
При более строгом соблюдении условий второй шаг недопустим, поскольку, когда сестра из первой пары вернется на левый берег, она окажется без сопровождения брата в присутствии мужчин, не состоящих с ней в родстве. В этом случае самое быстрое решение потребует одиннадцати переправ. Суть задачи о волке, козе и капусте состояла в том, что для переправы всего имущества через реку требовалось перевезти на другой берег один объект, затем вернуть его назад и снова перевезти. В данной задаче мы должны перевезти каждую сестру на другой берег, вернуть назад и снова переправить через реку.

Вот еще один из способов сделать это.

К тексту

Именно такое решение предложил Алкуин, оно же зашифровано в гекзаметре на латыни (в той версии, в которой пары состоят из мужа и жены). Вот примерный перевод этого гекзаметра.

Женщины, женщина, женщины, жена, мужчины, мужчина и жена,

Мужчины, женщина, женщины, мужчина, мужчина и жена.

К тексту

Стратегия, упомянутая мной в тексте, состоит в том, чтобы Джон, который ходит быстрее всех, перевел каждого из своих друзей через мост по одному. Джон переводит Пола за 2 минуты и возвращается за 1 минуту. Затем он переводит Джорджа за 5 минут и возвращается за 1 минуту. И наконец, переводит Ринго за 10 минут. Суммарное время составляет 2 + 1 + 5 + 1 + 10 = 19 минут.

Сначала эта стратегия кажется оптимальной без всяких доказательств. Почему бы не использовать каждый раз самого быстрого человека? Однако на самом деле целесообразнее собрать вместе двух человек, передвигающихся медленнее всех. Вот как это сделать:

1. Так же как и в предыдущем случае, Джон переводит Пола на другую сторону за 2 минуты и возвращается назад за 1 минуту.

2. Далее Джордж и Ринго переходят через мост вместе, что занимает у них 10 минут.

3. Они передают фонарь Полу, который возвращается по мосту, прибавив 2 минуты.