Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

К тексту

Эту веревку можно поднять примерно на 120 метров, что почти равно высоте небоскреба Centre Point, расположенного в центре Лондона. Такое расстояние кажется парадоксально большим. У нас есть веревка длиной 40 тысяч километров, натянутая вокруг Земли; удлиненная на один метр, она поднимется так высоко, что под ней пройдет пирамида из жирафов верхом на мотоциклах, на плечах которых стоит пирамида еще из двадцати жирафов. Теперь размер Земли становится непосредственным условием для ответа.

Вычисления требуют знания тригонометрии, слишком сложной для многих читателей. Так что если вы правильно вообразили эту задачу в графическом виде и подумали над тем, как ее решить, то уже заслуживаете высокой оценки.

На представленном рисунке r обозначает радиус Земли, а h – искомое решение, то есть максимальную высоту, на которую можно поднять веревку, не растягивая. Длина отрезка веревки от максимально высокой точки до Земли обозначена буквой t , а расстояние между точками касания Земли в тот момент, когда веревка висит в воздухе, равно двум g.

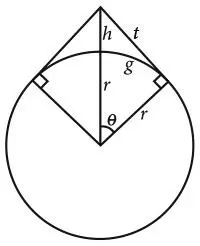
Мы можем найти h через r , но знайте: приятного в этом мало. И даже не пытайтесь что-то понять, если вы никогда не изучали тригонометрию. Сначала обратите внимание на то, что t – это касательная к поверхности Земли (а точнее, касательная к окружности, представляющей Землю на рисунке), поэтому имеем прямоугольный треугольник, в котором гипотенуза – это r + h , а две другие стороны – r и t. Воспользуемся теоремой Пифагора.

[1] t 2 + r 2 = (r + h) 2.

Мы знаем, что косинус угла θ равен r /( r + h ), значит,

[2] θ = arccos ( r /( r + h )).

А поскольку θ измеряется в радианах, то θ r = g. Тогда

[3] r arccos ( r /( r + h )) = g.

Из формулировки задачи нам известно, что

[4] 2 g + 1 = 2 t.

Эти уравнения можно перегруппировать и «упростить» (поверьте, это действительно возможно) до такого выражения: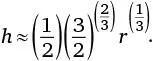

Если r = 6 400 000 метров, h ≈ 122 метра.

Вот и все. Я привел здесь эти вычисления для полноты картины, но обещаю, что в этой книге тригонометрии больше не будет.

К тексту

В этой задаче, как и в предыдущей, нужно опровергнуть интуитивные представления о пространстве. Высота шеста окажется немногим более семи метров, что примерно равно высоте викторианского дома на две спальни и гораздо выше роста самого высокого жирафа в мире. На удивление высокий шест, не так ли?

Теорема Пифагора позволяет нам получить результат без особых усилий. Как показано на рисунке, шест и гирлянда образуют два прямоугольных треугольника.

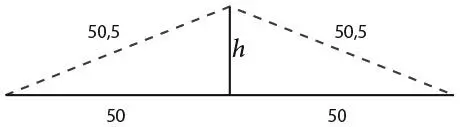
Каждая сторона гирлянды – это гипотенуза, а поверхность земли и шест – катеты. Следовательно:

h 2 + 50 2 = 50,5 2,

h 2 + 2500 = 2550,25.

Перегруппировав это уравнение, получаем:

h 2 = 2550,25 – 2550 = 50,25.

Таким образом, h = √50,25 = 7,1.

К тексту

Для того чтобы узнать, в каком направлении движется велосипед, сначала необходимо определить, где след переднего колеса, а где – заднего. Согласно дедуктивному методу, дорогой Ватсон, нам нужно понять, как кривая отпечатка колеса определяет его положение.

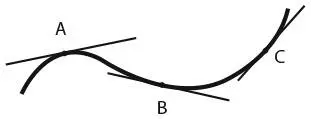
Если след колеса представляет собой прямую линию, значит, это колесо находится на одной линии с направлением следа. Если же след имеет вид кривой, то колесо, оставившее его, находится на одной линии с касательной этой кривой в каждой точке следа. (Касательная – это прямая, соприкасающаяся с кривой только в одной точке.) Для того чтобы понять, что я имею в виду, посмотрите на показанный на рисунке след, который мог бы оставить одноколесный велосипед. В точках A, B и C колесо велосипеда расположено на одной линии с касательными, изображенными на рисунке.

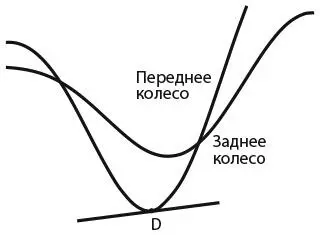
Обычно у велосипеда два колеса. Переднее может двигаться в любом направлении, а у заднего нет такой свободы: оно всегда движется в том же направлении, что и переднее.

Следовательно, где бы ни было заднее колесо, переднее всегда находится впереди точно на одну длину велосипеда в направлении касательной. Другими словами, все касательные к следу заднего колеса должны пересекать след переднего колеса, причем все они должны делать это на расстоянии одной длины велосипеда.

Теперь взгляните на точку D, отмеченную на жирной линии на рисунке ниже. В ней касательная не пересекает ни один след, что позволяет нам сделать следующий вывод: точка D находится не на линии следа заднего колеса, а на линии следа переднего колеса.

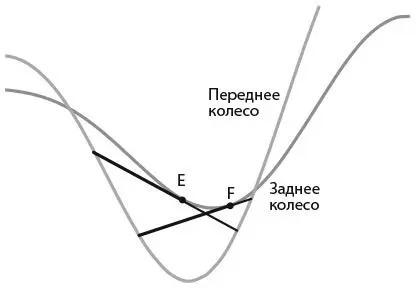
И наконец, мы можем определить направление движения велосипеда. Мы знаем, какой след оставило заднее колесо, а также, исходя из вышесказанного, что точка, расположенная на расстоянии одной длины велосипеда по любой касательной на этом следе в направлении движения, и есть точка на линии следа переднего колеса. А значит, нам остается только пройти по отрезкам касательных в обоих направлениях от точек E и F и узнать, где они пересекаются со следом от переднего колеса. Длина отрезков, отложенных от точек E и F в левую сторону, одинакова, а отложенных вправо – нет. Поскольку во время путешествия расстояние между колесами не меняется, велосипед передвигался справа налево. Элементарно, Ватсон!

К тексту

Я обожаю эту головоломку, потому что она иллюстрирует один любопытный феномен: верхняя часть колеса всегда движется быстрее, чем нижняя.

Когда колесо катится по горизонтальной поверхности, все точки на нем совершают движение в двух направлениях: перемещаются горизонтально, в направлении движения, и совершают вращательное движение вокруг центра колеса. Эти два направления движения совмещаются и в определенных случаях нейтрализуют друг друга. Рассмотрим такую точку. Когда она находится сверху (точка A на представленном рисунке), горизонтальное движение дополняет вращательное. Однако когда точка расположена внизу (точка B), вращательное движение направлено в сторону, противоположную горизонтальному, поэтому два движения нейтрализуют друг друга. С позиции наблюдателя точка в верхней части катящегося колеса всегда движется со скоростью, в два раза превышающей горизонтальную скорость колеса, а точка в нижней части колеса всегда неподвижна. Из этого следует, что точки в нижней части колеса перемещаются медленнее, чем в верхней.