Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления
- Название:Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2021
- Город:Москва
- ISBN:9785001468493
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления краткое содержание
Это книга для тех, кто интересуется математикой и логикой и любит разгадывать головоломки.
На русском языке публикуется впервые.
Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
На рисунке я обозначил пунктирной линией треугольник, длина гипотенузы которого равна b + a , поскольку она состоит из радиусов соответствующих кругов, а длина двух других сторон – b и 2 b – a. Вторую длину можно вывести исходя из того, что эта сторона треугольника равна половине стороны квадрата, длина которой должна быть равна 4 b , за вычетом радиуса круга A.
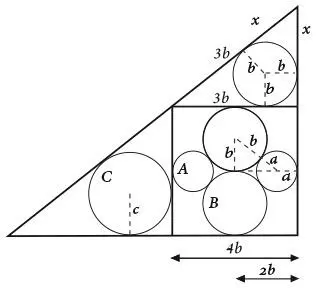
Теорема Пифагора гласит, что во всех прямоугольных треугольниках квадрат гипотенузы равен сумме квадратов катетов, а значит:
( b + a ) 2 = b 2 + (2 b – a ) 2.
Это уравнение можно представить в таком виде:
b 2 + 2 ab + a 2 = b 2 + 4 b 2 – 4 ab + a 2.
Сократим его до:
6 ab = 4 b 2.
Затем сократим еще раз:
3 a = 2 b.
И наконец, получим решение:
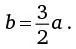
Таким образом, мы выразили b через a.
Теперь посмотрим на верхний треугольник на рисунке. Я построил отрезки от центра круга до каждой из его сторон. Каждый отрезок образует со стороной треугольника прямой угол, а значит, этот треугольник состоит из квадрата b × b и двух фигур в форме воздушного змея. Длинная сторона воздушного змея, смотрящая влево, составляет 3 b , поскольку она равна стороне большого квадрата минус радиус круга B. А исходя из того, что воздушные змеи симметричны, вторая сторона змея также должна быть 3 b. Если обозначить символом x сторону воздушного змея, смотрящую направо, то с помощью теоремы Пифагора получим:
(3 b + x ) 2 = ( b + x ) 2 + (4 b ) 2.
Раскрыв скобки в уравнении, будем иметь:
9 b 2 + 6 bx + x 2 = b 2 + 2 bx + x 2 + 16 b 2.
Сокращение даст нам следующий результат:
4 bx = 8 b 2.
Отсюда следует:
x = 2 b.
Вертикальная сторона верхнего треугольника равна x + b = 2 b + b = 3 b. Вертикальная сторона нижнего треугольника равна 4 b. Учитывая, что эти два треугольника одинаковой формы (хотя и разных размеров), соотношение их сторон, равное 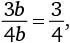 должно быть эквивалентно отношению радиусов кругов, вписанных в эти треугольники, равному b / c.
должно быть эквивалентно отношению радиусов кругов, вписанных в эти треугольники, равному b / c.
Если 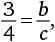 то
то 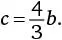
Теперь у нас есть c , выраженное через b , и b , выраженное через a. Следовательно, c можно выразить через a в таком виде: 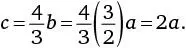
К тексту
37. ШАГАЯ ПО ТАТАМИ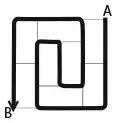
К тексту
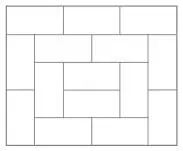
38. 15 ТАТАМИПредставленная на рисунке схема укладки татами взята из 1641-го издания самого популярного в Японии учебника математики XVII столетия под названием Jinkoki («Дзинкоки» – «Большие и малые числа»).
К тексту
39. ТАТАМИ НОБА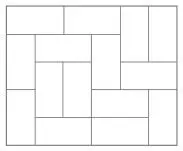
К тексту
40. КОМНАТА С ЛЕСТНИЦАМИ в углахПол комнаты размером 6 × 6 метров с вырезанными углами нельзя устелить семнадцатью татами. Раскрасив квадраты подобно клеткам на шахматной доске (как показано ниже), вы поймете почему. Каждый мат татами должен покрыть как серый, так и белый квадрат. Следовательно, чтобы устелить пол комнаты татами, в ней должно быть равное количество серых и белых квадратов. Но в этой комнате два дополнительных белых квадрата, поэтому решить головоломку невозможно.
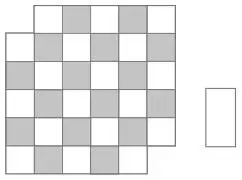
Как правило, в вариациях этой задачи используются костяшки домино и усеченная шахматная доска. Можно ли выложить костями домино размером в две шахматные клетки шахматную доску с вырезанными противоположными углами? Опять же ответ «нет» – по тем же причинам.
К тексту
41. КОМНАТА С ДВУМЯ ЛЕСТНИЦАМИ, РАСПОЛОЖЕННЫМИ В СЛУЧАЙНОМ ПОРЯДКЕМы решим эту задачу с помощью оригинального метода, придуманного Ральфом Гомори, который в 1970-х годах был директором IBM по исследованиям и разработкам. Хотя Гомори решал вариант этой головоломки с костями домино и шахматной доской, наше доказательство будет аналогичным. Для начала нарисуйте путь, который проходит через каждый квадрат только один раз, как показано на рисунке. На втором рисунке я в произвольном порядке удалил один серый и один белый квадрат, чтобы разместить там лестницы, разделяющие этот путь на два сегмента. Каждый из сегментов должен покрывать четное количество квадратов, а значит, его можно выстелить татами. Этот аргумент верен для всех путей и любых вариантов выбора двух квадратов разных цветов.
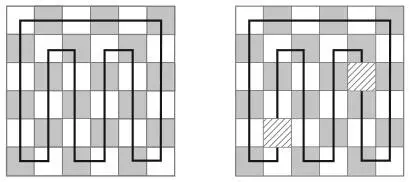
К тексту
42. ГОЛОВОЛОМКА С ДЕРЕВЯННЫМИ БЛОКАМИЭту задачу предложил сингапурец Джозеф Йоу Бун Вуй, автор головоломки о дне рождения Шерил (задача 21), который впервые прочитал о ней в 1980-х годах. Самое очевидное решение показано на рисунке А. Это так называемое слуховое (мансардное) окно – вертикальное окно, врезанное в скат крыши (как любезно подсказали мне многие из архитекторов). Задача решается еще двумя способами: B и C.

К тексту
43. КАРТИНА НА СТЕНЕЭту головоломку можно решить с помощью физики (фу!) или – математики (класс!). Как и следовало ожидать, первое решение менее изящное, чем второе. Забейте два гвоздя в стену настолько близко, чтобы часть веревки была крепко зажата между ними. Сложите веревку в форме буквы W посредине так, чтобы направленный вверх кончик буквы W находился между гвоздями. Картина будет висеть, поскольку гвозди держат веревку в нужном месте. Однако если вынуть один из гвоздей, она упадет. Некрасиво, но вполне эффективно.
А вот более элегантное решение.
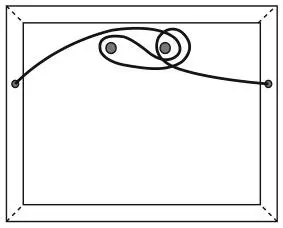
Впрочем, этот способ решения не один из моих любимых. Я надеялся, что вы используете для поиска ответа кольца Борромео, приняв во внимание мои прозрачные намеки на то, что эти кольца представляют собой математическую модель искомого решения. В случае удаления одного кольца два других разъединяются.
Читать дальшеИнтервал:
Закладка:









