Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

К тексту

3. в) 3, д) 5.

Буква e уже встречается в предложении восемь раз, поэтому предложение будет верным, если на месте пробела поставить слова nine (9) и eleven (11).

К тексту

4. B.

В местах пересечения разорванная линия нарисована первой, а сплошная проведена поверх нее. Следовательно, нам нужно найти маршрут, на котором линия разрывается, проходя любое пересечение впервые, и не разрывается, когда проходит через соответствующее пересечение во второй раз. Этому условию удовлетворяет только маршрут, который начинается в точке B и направлен от точки D.

К тексту

5. в) 45 × 56.

Из предложенных вариантов выражения 23 × 34, 56 × 67 и 67 × 78 не делятся на 5, поэтому их можно исключить из рассмотрения. Кроме того, число 34 не делится на 4, а 45 – нечетное число, так что выражение 34 × 45 тоже можно исключить, поскольку оно не делится на 4. Единственный оставшийся вариант – 45 × 56. Если представить это выражение в виде простых чисел, получится 45 × 56 = 2 3× 3 2× 5 × 7. Очевидно, что это число делится на все целые числа от 1 до 10 включительно, так как у нас есть простые числа 2, 3, 5 и 7, а остальные числа можно образовать из этой совокупности простых чисел: 4 = 2 2, 6 = 2 × 3, 8 = 2 3и 9 = 3 2.

К тексту

6. б) 2.

Если валет червей говорит правду, то лжет валет треф. Это означает, что валет бубен говорит правду, а валет пик лжет. С другой стороны, если валет червей лжет, то правду говорит валет треф; тогда лжет валет бубен, а валет пик говорит правду. В обоих случаях мы можем сказать, что два валета лгут, хотя нет возможности определить, кто именно.

К тексту

7. б) 3.

В каждом углу куба сходятся три грани, причем каждая пара граней имеет общее ребро. Следовательно, необходимо три разных цвета. Другие цвета не понадобятся при условии, что противоположные грани окрашены в такой же цвет, поскольку противоположные грани не имеют общих ребер.

К тексту

8. б) 100.

Если мой возраст сейчас – x , то возраст бабушки – 4 x. Пять лет назад 4 x – 5 = 5( x – 5). Сокращаем уравнение до x = 20. Следовательно, моей бабушке 80 лет, а мне 20 лет.

К тексту

9. б) –1.

Сначала сосредоточимся на младших (крайних правых) цифрах указанных чисел, то есть на 3, 5, 7 и 9, так как именно их нужно прибавить или вычесть, чтобы получить число, оканчивающееся на 0. Мы видим, что цифра 3 появляется первой, и это хорошо. Но если 3 + 7 = 10, то из 5 и 9 нельзя получить число, оканчивающееся на 0. Следовательно, мы должны выполнить операцию 3–7. И в нашем выражении перед числом 67 должен стоять знак минус. В таком случае 123 – 67 = 56. Далее нам необходимо получить недостающее число 44 из чисел 45 и 89. Единственный способ сделать это – из 89 вычесть 45. В итоге правильное выражение выглядит следующим образом: 123 – 45–67 + 89. В нем два знака минус и один знак плюс, а значит, p – m равно −1.

К тексту

10. a) 1:1.

Мы можем рассматривать эту схему укладки плитки как мозаику, составленную из фрагментов показанной ниже формы, а значит, искомое соотношение – 1:1.

К тексту

Как и в задаче о сотне кур, нам необходимо представить условия в виде двух уравнений: для птиц и для денег. Если количество уток, голубей и кур обозначить x, y и z , то получим:

[1] x + y + z = 100;

[2] 2 x + y /2 + z /3 = 100.

Сначала умножим уравнение [2] на 6, чтобы избавиться от дробей.

[3] 12 x + 3 y + 2 z = 600.

Кроме того, умножим уравнение [1] на 2, чтобы в нем было 2 z.

[4] 2 x + 2 y + 2 z = 200.

Теперь нам осталось только записать одно уравнение, сократив член 2 z. Преобразовав уравнение [3], получим 2 z = 600 – 12 x – 3 y , а подстановка этого выражения в уравнение [4] даст следующее:

2 x + 2 y + 600 – 12 x – 3 y = 200.

Это уравнение можно привести к такому виду:

[5] 10 x + y = 400.

Нам известно, что x y – целые числа меньше 100. Кроме того, мы можем сделать вывод в отношении y : значение этой переменной должно быть кратным 10. Поскольку 400 делится на 10, другая сторона уравнения 10 x + y тоже должна делиться на 10. Мы также знаем, что 10 x делится на 10, а значит, значение y также должно быть кратным 10, иначе 10 x + y не делилось бы на 10, а это противоречит тому, что нам известно.

Числа меньше 100, кратные 10, – это 10, 20, 30, 40, 50, 60, 70, 80 и 90. Однако y не может иметь значение 70, 80 или 90, потому что тогда значение x было бы 33, 32 и 31, а сумма x и y превысила бы 100. Шесть искомых решений выглядят так: y = 10, 20, 30, 40, 50 и 60, что дает нам следующее распределение птиц:

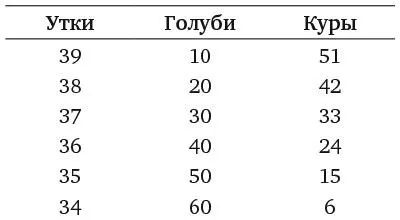
К тексту

Нам необходимо найти цену четырех товаров, но из условия задачи мы знаем только сумму и произведение их цен.

Давайте запишем уравнения. Пусть цены товаров – a, b, c и d. Кассир говорит, что:

[1] a × b × c × d = abcd = 7,11;

[2] a + b + c + d = 7,11.

Согласно основной теореме арифметики, каждое целое число равно произведению уникального множества простых чисел. Эта теорема будет весьма полезна, но мы пока не можем ее применить, поскольку она касается целых чисел, а произведение [1] – дробное число. Наша задача – превратить уравнение [1] в уравнение с целыми числами, что мы сделаем посредством следующих подстановок.

Пусть A = 100 a , B = 100 b , C = 100 c и D = 100 d. Умножив эти значения, получим:

[3] A × B × C × D = ABCD = 100 000 000 abcd.

Но мы знаем, что abcd = 7,11. Значит:

[4] ABCD = 711 000 000.

Теперь у нас есть число, с которым мы можем работать. Основная теорема арифметики говорит нам, что произведение уникального набора простых множителей, то есть простых чисел, равно числу 711 000 000. Эти множители можно найти вручную или, что предпочтительнее, с помощью компьютера:

711 000 000 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5 × 5 × 5 × 5 × 79.

Значит, ABCD = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5 × 5 × 5 × 5 × 79.

Таким образом, числа A, B, C, D состоят из простых чисел. Вопрос в том, как определить, произведение каких чисел дает значение A, произведение каких чисел равно значению B, произведение каких чисел образует C и произведение каких чисел равно D. Другими словами, как соотнести эти числа со значениями A, B, C, D?

Теперь вернемся к уравнению [2] и умножим его на 100, чтобы получить второе уравнение с A, B, C, D:

[5] 100 a + 100 b + 100 c + 100 d = A + B + C + D = 711.

То есть мы должны распределить приведенные выше простые числа между A, B, C и D так, чтобы их сумма составляла 711.

Плохо, что здесь нет короткого пути, – необходимо просто применить метод проб и ошибок. Предположим, например, что A = 2 × 2 × 2 × 2 × 2 × 2 = 64, B = 3 × 3 = 9, C = 5 × 5 × 5 × 5 × 5 × 5 = 15 625 и D = 79. В таком случае A + B + C + D = 15 777, а значит, мы сделали неправильный выбор.