Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

К тексту

Давайте пронумеруем монеты от 1 до 12.

Во время первого взвешивания нам нужно сравнить вес монет 1, 2, 3, 4 и 5, 6, 7, 8. Если чаши весов уравновешены, значит, фальшивая монета находится среди оставшихся – 9, 10, 11 и 12.

Возьмем три из этих монет и сравним их вес с любыми тремя уже взвешенными монетами, среди которых, как нам известно, фальшивых нет. Предположим, это монеты 1, 2, 3 и 9, 10, 11.

Если чаши весов находятся в равновесии, значит, фальшивая монета – 12. А чтобы определить, легче или тяжелее она остальных, во время третьего, последнего взвешивания необходимо сравнить ее вес с весом любой другой монеты.

В случае если чаши весов не уравновешены, фальшивой монетой будет 9, 10 или 11. А легче она или тяжелее остальных, зависит от того, поднялась ли чаша весов с монетами 9, 10 и 11 или опустилась. Теперь возьмем любую из монет 9, 10, 11 и сравним вес двух из них, отложив третью монету в сторону (так же как мы сделали с девятью монетами в задаче Баше о взвешивании). В случае равновесия чаш весов оставшаяся монета – фальшивая. Если нам известно, что фальшивая монета легче, то она будет лежать в поднятой чаше. Если нам известно, что фальшивая монета тяжелее, то она лежит в опущенной чаше.

Решение несколько усложняется, если после первого взвешивания монет 1, 2, 3, 4 и 5, 6, 7, 8 весы не уравновешены.

Представьте себе, что чаша весов с монетами 1, 2, 3, 4 ниже чаши с монетами 5, 6, 7, 8.

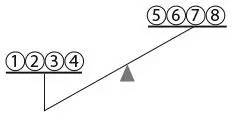
Следовательно, 9, 10, 11 и 12 – не фальшивые монеты.

Для второго взвешивания возьмем одну из правильных монет (например, монету 9) и поместим ее на чашу весов вместе с двумя монетами из той чаши, которая опустилась при первом взвешивании (скажем, вместе с монетами 1 и 2). Две оставшиеся монеты из опустившейся чаши (монеты 3 и 4) положим на другую чашу вместе с одной монетой из поднявшейся чаши (скажем, с монетой 5). Монеты с номерами 6, 7 и 8 не участвуют во взвешивании.

Вот три возможных итога второго взвешивания:

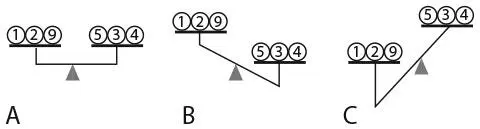
Вариант А. Весы уравновешены. Значит, фальшивая монета – это 6, 7 или 8. При третьем взвешивании сравните вес монет 6 и 7. Если весы уравновешены, фальшивой монетой будет 8, причем она легче остальных, поскольку чаша весов с ней поднялась при первом взвешивании. Если чаша весов с монетой 6 поднимется, то это и есть фальшивка, а если опустится, то наша правонарушительница – монета 7.

Вариант В. Левая чаша поднимается. В таком случае фальшивая монета должна быть среди монет 1, 2, 3, 4 и 5, а значит, мы можем исключить 6, 7 и 8 из рассмотрения.

Если одна из монет 1, 2, 3, 4 фальшивая, она должна быть тяжелее остальных, поскольку чаша весов с монетами 1, 2, 3, 4 опустилась при первом взвешивании. Следовательно, фальшивой должна быть либо монета 3, либо монета 4. Сравните их вес при третьем взвешивании.

Вариант С. Правая чаша поднимается. Как и в варианте В, фальшивой должна быть одна из этих пяти монет, поэтому мы можем исключить из рассмотрения монеты 6, 7 и 8. И, как и в варианте В, если одна из монет 1, 2, 3, 4 фальшивая, она должна быть тяжелее остальных, потому что чаша весов с монетами 1, 2, 3, 4 опустилась при первом взвешивании. Следовательно, фальшивой может быть монета 1 или 2.

Но остается еще одна возможность. Поскольку чаша весов с монетами 5, 6, 7 и 8 поднялась при первом взвешивании, монета 5 могла бы быть фальшивой и более легкой.

Таким образом, во время последнего взвешивания необходимо сравнить вес монет 1 и 2. Фальшивой будет та, которая лежит в опустившейся чаше, поскольку если чаши весов уравновешены, то правонарушительница – монета 5.

Если после первого взвешивания чаша весов с монетами 1, 2, 3, 4 окажется выше чаши с монетами 5, 6, 7, 8, следует повторить описанные выше действия, поменяв местами монеты 1, 2, 3, 4 и 5, 6, 7, 8.

К тексту

Разумеется, одно взвешивание!

Положите на весы одну монету из первой стопки, две из второй, три из третьей, четыре из четвертой и так далее до тех пор, пока не выложите десять монет из последней стопки. На весах будет 1 + 2 + 3 + 4 + … + 10 = 55 монет.

Поскольку вам известен вес одной монеты, то вы знаете и общий вес 55 монет. Разность в граммах между весом на весах и весом 55 монет – и есть номер стопки с фальшивыми монетами. Если эта разность составляет 1 грамм, на весах всего одна фальшивая монета и лежит она в первой стопке; если разность составляет 2 грамма, то на весах две фальшивые монеты, а стопка с фальшивыми монетами – вторая, и т. д.

К тексту

Впервые узнав об этой головоломке, я сразу же подумал, что ответ – 7; такой же ответ дали и те выдающиеся французские математики, которым эту задачу задал Эдуард Люка.

Путь через океан занимает семь дней. Следовательно, семь лайнеров, которые вы встретите на своем пути, отправятся из Нью-Йорка сегодня, завтра и в следующие дни до тех пор, пока не отправится лайнер в день накануне вашего прибытия.

Но это неправильный ответ! А как же те лайнеры, что отправились из Нью-Йорка на прошлой неделе? Они плывут сейчас в открытом море, и вы, конечно, тоже встретите их. Правильный ответ: в момент отплытия из Гавра вы встретите первый лайнер в порту (этот корабль, отправившийся из Нью-Йорка неделю назад, прибудет в полдень), еще 13 лайнеров в открытом море и последний корабль в Нью-Йорке, откуда он отправится в тот момент, когда вы туда прибудете в полдень через неделю. Все это хорошо видно на рисунке.

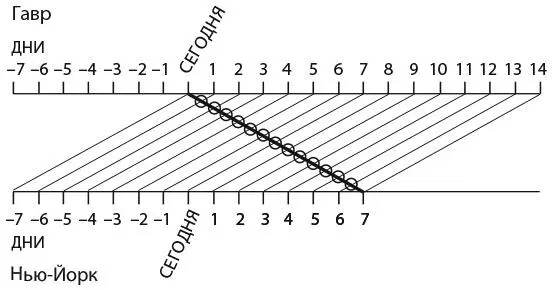
Если все океанские лайнеры перемещаются с постоянной скоростью, вы будете встречать один лайнер каждые 12 часов – один раз в полдень (по времени Гавра) и один раз в полночь.

К тексту

Допустим, ветер дует в направлении движения самолета из пункта А в пункт Б и против движения самолета на обратном пути.

Создается впечатление, что ускорение попутного ветра и сопротивление встречного должны уравновесить друг друга, поскольку скорость, которую придает самолету попутный ветер в одном направлении, нейтрализует ветер на обратном пути. Если скорость ветра равна W, то скорость самолета на пути из пункта А в пункт Б увеличивается на W, а на обратном пути снижается на W.

Однако здесь важна не скорость, а продолжительность полета. Времени, сэкономленного за счет более быстрого полета, меньше, чем времени, потерянного из-за сопротивления ветру, потому что с более низкой скоростью самолет летит дольше.

Мы можем понять это, подставив несколько чисел. Самолет, летящий со скоростью 500 миль в час, пролетает 500 миль за один час. Если он преодолевает то же расстояние со скоростью, на 100 миль в час большей, ему понадобится на 10 минут меньше времени. (Время = расстояние ÷ скорость. Следовательно, если расстояние составляет 500 миль, а скорость – 600 миль в час, то есть 10 миль в минуту, то продолжительность полета в минутах составит 500 ÷ 10 = 50 минут.)