Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Если скорость самолета на 100 миль в час меньше, то его полет будет на 15 минут дольше. (Если расстояние 500 миль, а скорость 400 миль в час, то продолжительность путешествия в часах равна 500 ÷ 400 = 1,25, или один час с четвертью.)

Таким образом, полет на расстояние 500 миль туда и обратно при скорости ветра 100 миль в час занял бы в целом на пять минут больше времени, чем при полном отсутствии ветра.

Однако даже без всех этих вычислений представьте, что произошло бы, если бы скорость ветра была равна скорости самолета. Самолет преодолел бы путь из пункта А в пункт Б за половину времени. Но на обратном пути его скорость равнялась бы нулю, и он даже не оторвался бы от взлетной полосы!

Конечно, это крайний случай, но он показывает закономерность. Повышая скорость на определенную величину, вы не сможете сэкономить больше времени, чем время полета, а вот снижая скорость на такую величину, можете потерять целую жизнь. Таким образом, если ветер дует в направлении движения самолета, то полет в два конца займет больше времени, чем при полном отсутствии ветра.

А что же боковой ветер? Он может дуть как по курсу движения самолета (или против него), так и перпендикулярно его движению. Поскольку мы знаем, что в первом случае продолжительность маршрута в оба конца увеличивается, что мы можем сказать о втором сценарии? Для того чтобы пролететь по прямой из пункта А в пункт Б при боковом ветре, дующем перпендикулярно, пилоту необходимо вести самолет под углом к направлению ветра, а значит, часть скорости будет потрачена на преодоление ветра, а не на перемещение из пункта А в пункт Б. Так что путешествие туда и обратно тоже займет больше времени.

Лучший сценарий для полета в оба конца – полное отсутствие ветра.

К тексту

Прежде всего нужно понять, что первые четыре цифры одометра станут одинаковыми после того, как автомобиль проедет тысячу миль, а счетчик пробега за одну поездку обнулится. К этому моменту он проделает 876,6 мили, которые мы получим, вычислив разность 1000 – 123,4, и приборная панель будет выглядеть так:

Еще через 130 миль станут одинаковыми первые две цифры.

А еще через 3,0 мили мы получим искомый ответ.

Первые четыре цифры снова одинаковые, при этом автомобиль проехал 1010,1 мили.

К тексту

Головоломки такого рода несложные, но именно из-за кажущейся легкости ленивый мозг не анализирует их достаточно тщательно.

1. Обогнав человека, бегущего вторым, вы оказываетесь на втором месте.

2. Обогнать последнего бегуна невозможно, поскольку, если бы за ним кто-то бежал, он не был бы последним.

К тексту

Еще одна замечательная головоломка, противоречащая здравому смыслу, поскольку кажется невозможным, чтобы Дафни, которая пробегает каждую милю за 8 минут 1 секунду, победила Констанс, пробегающую каждую милю за 8 минут. Однако Дафни, конечно же, может это сделать, иначе не было бы задачи.

Как бы парадоксально это ни звучало, бегун, который медленнее преодолевает каждую милю, может найти способ пробежать быстрее дистанцию 26,2 мили. Давайте проанализируем, как Дафни бежит марафон. Она бежит не с постоянной скоростью, но при этом преодолевает каждую милю за одинаковое время. Как ей это удается?

Посмотрите на рисунок, на котором отображена скорость передвижения бегуна на протяжении всего забега. На нем вы видите стратегию, в соответствии с которой первый участок а каждой мили преодолевается с высокой скоростью, а оставшаяся часть мили – с постоянной низкой скоростью. При использовании этой стратегии на каждой миле забега бегун преодолевает общую дистанцию не с постоянной скоростью, однако каждый отрезок длиной в милю будет пройден за одно и то же время. Это объясняется тем, что, какую бы милю мы ни взяли, часть а этой мили преодолевается с высокой скоростью, а остаток – с низкой.

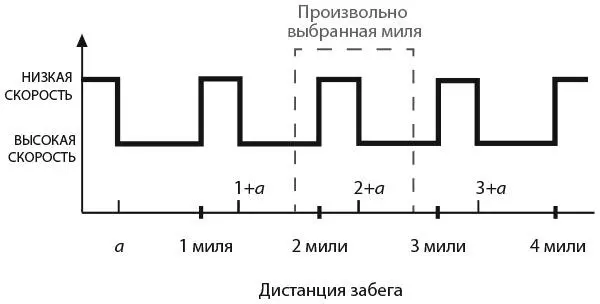
При условии, что Дафни будет использовать в марафоне такую стратегию, попробуем максимально адаптировать ее к нуждам бегуньи. Дистанция забега – 26,2 мили. Поскольку Дафни проигрывает Констанс по одной секунде на каждой полной миле, на отметке 26 миль она проиграет 26 секунд. Следовательно, нашей бегунье необходимо наверстать их на оставшемся участке длиной 0,2 мили.

Предположим, стратегия Дафни – бежать с высокой скоростью первые 0,2 каждой мили и с низкой скоростью оставшуюся часть. Теперь нам необходимо говорить скорее о времени , а не о скорости. Пусть Дафни пробегает первые 0,2 мили за x секунд, а оставшиеся 0,8 мили за y секунд. Следовательно, она пробегает каждую милю за x + y секунд.

В формулировке задачи сказано, что Дафни пробегает каждую милю за 8 минут 1 секунду, то есть за 481 секунду. Получаем следующее уравнение:

[1] x + y = 481

Констанс пробегает каждую милю за 8 минут, а весь марафон преодолевает за 26, 2 × 8 × 60 секунд, или 12 576 секунд.

Допустим, Дафни выиграет марафон, опередив соперницу всего на одну секунду, то есть пробежит его за 12 575 секунд. Поскольку она пробегает первые 0,2 мили дистанции длиной в одну милю 27 раз, а 0,8 мили только 26 раз, мы получаем следующее уравнение:

[2] 27 x + 26 y = 12 575.

Мы без труда можем решить эту систему уравнений. Из уравнения [1] получаем y = 481 – x. Подставим это значение y в уравнение [2]. После сокращения его членов остается x = 69 секунд и y = 412 секунд. Следовательно, если Дафни будет быстро пробегать 0,2 каждой мили за 69 секунд, а затем преодолевать оставшиеся 0,8 мили за 412 секунд, на каждой миле она будет проигрывать, но в самом конце опередит Констанс на одну секунду.

К тексту

Ответ – 50 килограммов. Картофель теряет половину веса! В этой задаче интересно то, что столь большая потеря в весе кажется противоречащей здравому смыслу.

Вычисления, которые позволят нам получить правильный ответ, достаточно просты. Вода составляет 99 процентов картофеля. Назовем оставшийся 1 процент картофельным экстрактом.

Вес картофеля – 100 килограммов, и он состоит из 1 килограмма картофельного экстракта и 99 килограммов воды. Соотношение экстракта и воды – 1: 99. После испарения на воду приходится только 98 процентов веса картофеля, значит, соотношение меняется на 2: 98, и это то же самое, что 1: 49. Поскольку вес картофельного экстракта по-прежнему равен 1 килограмму, количество воды должно сократиться до 49 килограммов, а значит, общий вес картофеля составит 1 + 49 = 50 килограммов [41].