Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления
- Название:Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2021
- Город:Москва
- ISBN:9785001468493
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления краткое содержание
Это книга для тех, кто интересуется математикой и логикой и любит разгадывать головоломки.
На русском языке публикуется впервые.
Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Если же A займет место Z, то, очевидно, Z не займет свое место, поскольку его уже занял A. В этом случае Z сядет на место A.
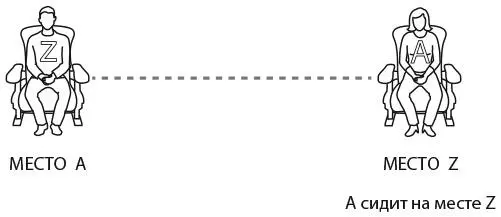
В задаче сказано, что посетитель A выбирает место случайным образом, а значит, он с равной вероятностью может занять как место A, так и место Z. Если ограничиться в ходе рассуждений только этими двумя местами, то Z займет свое место с вероятностью 50: 50.
А что, если A займет любое другое место. Предположим, место посетителя N, который занимает n -е место в очереди.
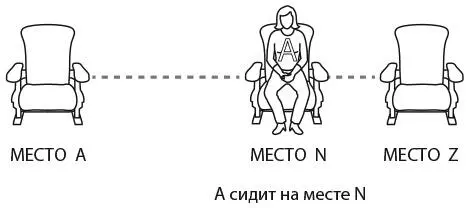
Если A сидит на месте N, то все люди, которые стоят в очереди до N, займут места, указанные в их билетах. Первым, кто не сядет на свое место, будет N, поскольку его место уже занял A. В итоге N выберет одно из оставшихся мест.
Теперь N может расположиться на месте A и местах тех, кто стоит в очереди после него, в том числе Z. Следовательно, N займет либо место A (в таком случае Z в итоге сядет на правильное место), либо место Z (в этом случае Z не сядет на свое место). Или же N сядет на место M, где M – зритель, который стоит в очереди после N, но раньше Z.
Если ограничиться размышлениями о том, займет ли N место A или Z, шансы в обоих случаях равны, а значит, Z займет свое место с вероятностью 50 процентов. А что, если N сядет на место M?
Когда наступит очередь посетителя M занять свое место, он столкнется с таким же выбором, что и N: у него есть равные шансы занять либо место A, либо место Z или шанс занять место того посетителя театра, который еще должен войти в зал. Если M займет место еще не вошедшего посетителя, сценарий повторится.
На каждом этапе любой зритель выберет либо место A, либо место Z с равной вероятностью. А если этот зритель выберет чье-то место, то решение о выборе между A и Z откладывается до следующего, кто войдет в зал. В конечном счете мы переберем всех, и кому-то придется сесть либо на место A, либо на место Z.
У любого посетителя театра, вынужденного сесть на случайное место, всегда равные шансы выбрать место A или место Z. В случае выбора места A посетитель Z займет свое место, а при выборе места Z – не свое. Таким образом, вероятность того, что Z сядет на свое место, составляет 50 %.
К тексту
1. Рим.
К тексту
2. Мэн, поскольку североатлантическое побережье США простирается на восток дальше, чем кажется.
К тексту
3. Глазго, Плимут, Эдинбург, Ливерпуль, Манчестер.
К тексту
4. Париж, Сиэтл, Галифакс, Алжир, Токио.
К тексту
5. Остров Пасхи, Перт, Кейптаун, Буэнос-Айрес, Монтевидео.
К тексту
6. Германия. У этой страны девять соседей (по часовой стрелке): Дания, Польша, Чехия, Австрия, Швейцария, Франция, Люксембург, Бельгия, Нидерланды.
К тексту
7. В порядке возрастания численности населения: Фолклендские острова, Шетландские острова, остров Мэн, Джерси, остров Уайт.
К тексту
8. Канада.
К тексту
9. Интересно, что один часовой пояс задекларирован в Китае, хотя протяженность этой страны с востока на запад составляет 4828 километров, причем это расстояние больше, чем расстояние от Лондона до Москвы.
К тексту
10. Аконкагуа – 6962 метра; Мак-Кинли – 6194 метра; Килиманджаро – 5892 метра; Эльбрус – 5642 метра.
К тексту
Сначала выложите монеты в форме параллелограмма, как показано на рисунке. Каждое перемещение обозначено стрелкой.
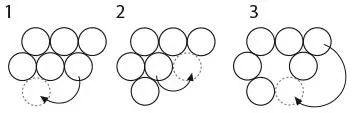
К тексту
77. ПРЕВРАЩЕНИЕ ТРЕУГОЛЬНИКА В ЛИНИЮ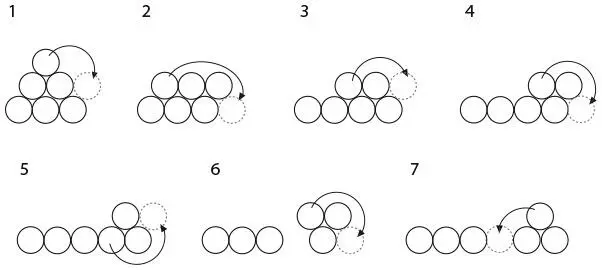
К тексту
78. ВОДНАЯ ГОЛОВОЛОМКА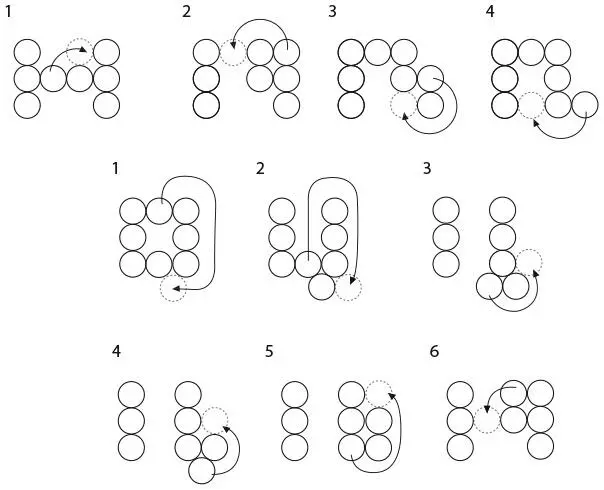
К тексту
79. 5 ПЕННИ
Решение Дьюдени состояло в том, чтобы положить одну монету горизонтально на стол, а затем еще две монеты разместить горизонтально сверху. И еще две монеты расположить так, чтобы они касались друг друга вверху и трех других монет внизу. Сделать это трудно, но возможно! В книге «Токийские головоломки» Кобон Фуджимура говорит, что один из его читателей прислал вариант решения, в котором только одна монета стоит на ребре.
К тексту
80. ПОСАДИТЕ 10 ДЕРЕВЬЕВ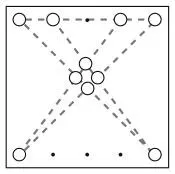
Решение начинается с двух линий, на которых расположено по пять монет; а нужно выстроить пять линий по четыре монеты в каждой.
Вы можете менять положение только четырех монет. Пожалуй, стоит взять одну монету из одной линии с пятью монетами, что дает нам первую линию с четырьмя монетами, а оставшиеся три – из другой линии с пятью монетами.
На рисунке вы видите, что можно выстроить четыре новые линии по четыре монеты, соединив каждую монету на первой линии с четырьмя монетами с одной из двух расположенных напротив монет. В этом решении я переместил среднюю монету из верхнего ряда и три средних монеты из нижнего ряда. Вообще-то я мог бы переместить любую монету из верхнего (или нижнего) ряда и любые три монеты из нижнего (или верхнего) ряда. Вот еще два возможных решения.
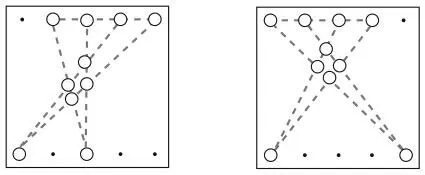
Так сколько возможных вариантов решений? Существует пять способов выбрать одну монету из ряда с пятью монетами, а также десять способов выбрать три монеты из ряда с пятью монетами, следовательно, есть 5 × 10 = 50 способов выбрать одну монету из верхней линии и три из нижней, что дает нам 50 решений. К этому можем добавить еще 50 решений в случае выбора одной монеты из нижней линии и трех монет из верхней, что дает нам всего 100 решений.
Я принимаю этот ответ. Однако я дал бы вам дополнительные баллы, если бы вы поняли, что каждое из этих ста решений можно выполнить 24 способами, поскольку четыре передвинутые монеты можно расположить 24 возможными способами. Например, посмотрите на первое решение, представленное на рисунке выше, где перемещенные монеты расположены в форме ромба. Если обозначить монеты символами A, B, C и D и начать их передвигать, скажем, с верхней позиции по часовой стрелке, то получим в первом случае монеты, расположенные в порядке ABDC, во втором – ACBD и т. д.; всего 24 комбинации A, B, C и D.
Читать дальшеИнтервал:
Закладка:









