Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

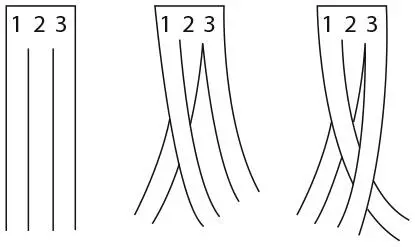
Я уже говорил, что пряди в косе переплетаются шесть раз. Это подсказка. Давайте забудем на минуту, что три полосы соединены у верхних и нижних концов. Начните заплетать косу сверху. Наложите полосу 1 на полосу 2, затем полосу 3 на полосу 1 и сделайте еще четыре переплетения, пока не получите все шесть. (Это достаточно кропотливая работа, поэтому я рекомендую использовать пластиковую полосу, так как бумага может порваться.) Зажав шестое переплетение большим и указательным пальцами, вы получите нечто напоминающее причудливо скрученный узел, как показано на рисунке ниже.

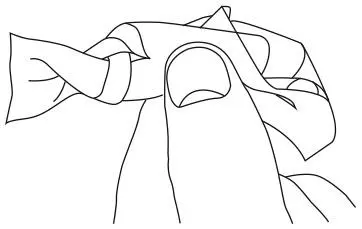
Этот узел получился в результате того, что при каждом переплетении полос в верхней части в нижней происходило их безобразное скручивание. После шести переплетений то, что получилось слева от большого пальца, представляет собой схему нашего решения, а то, что справа, – просто ком пластика.

Что же делать дальше? Попытайтесь распутать свободной рукой тот бесформенный ком, который образовался с правой стороны. Если пропустить правый конец несколько раз через себя, полосы полностью распутаются. Поправьте косу так, чтобы «пряди» были сплетены равномерно. В конечном счете невозможная коса все же возможна.

Хотя это решение не очень изящное, но оно работает. Порой решение задачи сводится к выполнению самого простого действия. В задаче сказано сплести косу – так делайте это!

К тексту

1. б) 1.

Все эти утверждения противоречат друг другу, а значит, истинным может быть не более чем одно из них. А если одно из утверждений истинно, то оно должно быть вторым, поскольку это действительно так.

К тексту

2. а) равносторонний треугольник.

Если эта фигура – треугольник, то две из его сторон должны быть смежными сторонами квадрата, один из углов которого будет составлять 90 градусов. Следовательно, равносторонний треугольник, у которого все углы составляют 60 градусов, не может образоваться при наложении двух квадратов. На рисунке показано, какие фигуры могут получиться при разных способах наложения двух одинаковых квадратов.

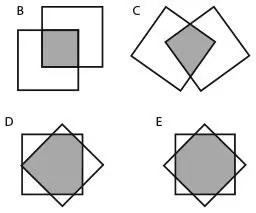
К тексту

3. г) 88 2 + 33 2 = 8833

Проанализируем цифры разряда единиц с каждой стороны уравнения, так как именно они скажут нам, какое уравнение правильное. Цифра разряда единиц 44 2 + 77 2 – 5, поскольку цифра разряда единиц 4 2 – 6, а цифра разряда единиц 7 2 – 9. Цифра разряда единиц 55 2 + 66 2и 66 2 + 55 2 – 1, а цифра разряда единиц 99 2 + 22 2 – 5. Следовательно, все эти утверждения ложные. И наконец, нам необходимо проверить, действительно ли 88 2 + 33 2 = 7744 + 1089 = 8833.

К тексту

4. г) 13.

Очевидно, что как минимум два переключателя должны быть в положении «включен». Два переключателя в положении «включен» и три переключателя в положении «выключен» можно установить только одним способом: выключен, включен, выключен, включен, выключен. Три переключателя в положении «включен» и два переключателя в положении «выключен» можно расположить шестью разными способами. Четыре переключателя в положении «включен» и один переключатель в положении «выключен» могут быть установлены пятью разными способами. И наконец, пять переключателей в положении «включен» могут располагаться одним способом. Итого 1 + 6 + 5 + 1 = 13 способов.

К тексту

5. д) 42.

Рассмотрим столбец тысяч. Буквами обозначены разные цифры. Поскольку S = 3, M может быть 0, 1 или 2. Мы можем исключить 0 и 1, так как S должно отличаться от М только на 1 перенос из предыдущего разряда. Следовательно, M = 2 при условии переноса 1 из столбца сотен. A = 9, потому что только при этом значении можно перенести 1 в следующий разряд, если из разряда десятков также был сделан перенос 1. Таким образом, U должно обозначать 0. В столбце десятков N должно обозначать 8 с переносом 1; это не может быть 9, поскольку эта цифра уже использовалась. Остается O + Y = 13. Пары чисел, которые подходят для O и Y, – это 4 и 9 (или наоборот), 5 и 8 (или наоборот), а также 6 и 7 (или наоборот). Однако 8 и 9 уже использовались, так что это должен быть последний вариант: 6 × 7 = 7 × 6 = 42.

К тексту

6. г) 3.

Это происходит только в случаях, когда показания на часах меняются с 09:59:59 на 10:00:00; с 19:59:59 на 20:00:00 и с 23:59:59 на 00:00:00.

К тексту

7. г) 216.

Первые шесть положительных кубов – это 1, 8, 27, 64, 125 и 216. Очевидно, что 64 не может быть суммой трех положительных кубов, поскольку сумма всех положительных кубов меньших 64 равна 1 + 8 + 27 = 36. Аналогичным образом 125 не может быть суммой трех положительных кубов, поскольку максимальная сумма любых трех положительных кубов меньших 125 равна 8 + 27 + 64 = 99. Однако 27 + 64 + 125 = 216, а значит, 216 – это и есть наименьший куб, представляющий собой сумму трех положительных кубов.

К тексту

8. в) 13-й.

Если первые три члена последовательности – это −3, 0, 2, то четвертый член – это −3 + 0 + 2 = −1. Следовательно, пятый член – 0 + 2–1 = 1 и т. д. Первые тринадцать членов этой последовательности: –3, 0, 2, –1, 1, 2, 2, 5, 9, 16, 30, 55, 101…

К тексту

9. в) 320.

Для того чтобы пронумеровать страницы с 1-й по 9-ю, нам понадобится 9 цифр; для нумерации страниц с 10-й по 99-ю необходимо 180 цифр. Таким образом, для нумерации страниц до начала трехзначных чисел (со страницы 100) потребуется 189 цифр. Остается 663 цифры, на которые приходится еще 221 страница. Следовательно, в книге 9 + 90 + 221 = 320 страниц.

К тексту

10. б) 18.

Представьте, что этот крест состоит из трех горизонтальных уровней. На первом расположен куб, который был приклеен к верхней грани исходного куба. На втором находится исходный куб и четыре дополнительных куба, приклеенных к его боковым граням. Третий уровень содержит только куб, приклеенный к нижней грани исходного куба. При добавлении желтых кубов один куб приклеивается к верхней грани голубого куба на первом уровне и четыре куба – к его боковым граням. Восемь желтых кубов будут приклеены к голубым кубам на втором уровне. А к единственному голубому кубу на третьем уровне будут приклеены пять желтых кубов, как и в кубе на первом уровне. Следовательно, всего потребуется 18 желтых кубов.

К тексту

Эти суммы одинаковые! Такой вывод кажется довольно неожиданным, пока вы не проанализируете вычисления по столбцам. Может, даже целесообразно произнести это вслух. Первый столбец суммы слева содержит одну девятку, или 1 × 9; первый столбец суммы справа содержит девять единиц, или 9 × 1. Второй столбец суммы слева содержит две восьмерки, или 2 × 8; второй столбец суммы справа содержит восемь двоек, или 8 × 2. И так далее. Цифры в каждом столбце дают в сумме одно и то же число, а значит, общие суммы одинаковы.