Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Ну, не совсем. Число

10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000, или – это googol (гугол), а в этом слове шесть букв. Если прибавить к этому числу еще один ноль, получится число ten googol (десять гуголов), а здесь девять букв. Вот это лучший ответ!

Понимаете, почему эту задачу, как утверждают некоторые, часто просят решить в Google потенциальных кандидатов?

К тексту

В словаре один квадриллион чисел. Все числа должны начинаться с одного из слов one (1), two (2), three (3), four (4), five (5), six (6), seven (7), eight (8), nine (9), ten (10), eleven (11), twelve (12), thirteen (13), fourteen (14), fifteen (15), sixteen (16), seventeen (17), eighteen (18), nineteen (19), twenty (20), thirty (30), fourty (40), fifty (50), sixty (60), seventy (70), eighty (80) или ninety (90). Следовательно, номер первой словарной статьи должен начинаться с цифры 8.

Аналогичные рассуждения позволяют сделать вывод, что номер последней словарной статьи должен начинаться с цифры 2, поскольку из всех перечисленных выше слов two – последнее по алфавиту. Однако это неправильный ответ, так как числа, начинающиеся с 2, но не являющиеся этим числом, будут расположены в словаре после числа 2. Существуют такие варианты для следующего обозначения искомого числа: trillion (1 000 000 000 000), billion (1 000 000 000), million (1 000 000), thousand (1000) и hundred (100). Слово trillion (1 000 000 000 000) последнее по алфавиту, а значит, первые два слова искомого числа – two trillion (2 000 000 000 000). Следующее слово в этом числе также должно быть two. Далее идут слова thousand (1000), two (2), hundred (100), two (2). Ответ – 2 000 000 002 202.

Первая нечетная словарная статья должна начинаться с 8, но, очевидно, это не 8, поскольку число четное. Варианты для следующего слова, обозначающего искомое число, – снова trillion (1 000 000 000 000), billion (1 000 000 000), million (1 000 000), thousand (1000) и hundred (100); ближе всего к началу алфавита находится слово billion (1 000 000 000). Следующие пять букв должны быть eight, а значит, возможны только такие варианты: eighteen (18), eighty (80), eight million (8 000 000), eight thousand (8000) или eight hundred (800). Побеждает eighteen (18). Продолжив, получим: million (1 000 000), eighteen (18), thousand (1000), eight (8), hundred (100), eighty (80). На этот момент наше число – 801 801 888 х , где х – последняя цифра. Число нечетное, значит, мы должны выбрать один из вариантов one (1), three (3), five (5), seven (7) и nine (90). Побеждает five (5).

Следовательно, ответ – 8 018 018 885.

Для того чтобы определить последнюю словарную статью, соответствующую нечетному числу, необходимо проделать то же самое. В итоге будет получено число 2 000 000 002 203.

ЗАДАЧА В ПРИДАЧУ: SEND MORE MONEY

Мы получили следующий результат:

Если в разряде тысяч есть перенос, то 1 + 9 + 1 = 1O (где О – заглавная буква «о»). Однако в этом случае О = 1, что невозможно, поскольку М = 1. Следовательно, в разряде тысяч нет переноса, а значит, О = 0.

Это нам только на пользу, потому что путаница между нолем и буквой «о» только мешает! Однако должен быть перенос в разряде сотен, так как в противном случае E + 0 = N, а значит, E = N, что невозможно, ввиду того что две буквы не могут быть обозначены одним и тем же числом. Теперь сумма выглядит так:

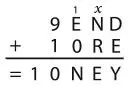
Я прибавил также х там, где должен быть перенос в столбце десятков. Если перенос есть, то х = 1, иначе х = 0. Я прибавил х , потому что это позволяет записать следующие три уравнения, соответствующие оставшимся столбцам.

Столбец сотен: E + 1 = N.

Столбец десятков: + N + R = 10 + E (10 представляет перенос).

Столбец единиц: D + E = Y + 10 х.

Если х = 0, то, подставив E + 1 вместо N во втором уравнении, получим:

E + 1 + R = 10 + E, что можно упростить до R = 9.

Этот результат невозможен, поскольку S = 9. Следовательно, х = 1, что дает нам три уравнения:

E + 1 = N

N + R = 9 + E

D + E = Y + 10

Подставив E + 1 вместо N во втором уравнении, получим E +1 + R = 9 + E и упростим выражение до R = 8.

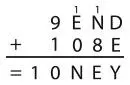
У нас остается:

E + 1 = N

D + E = Y + 10

Цифры 0 и 1 уже использовались, значит, Y должно быть равным 2 или больше. Следовательно, D + E ≥ 12. Поскольку 9 и 8 уже задействованы, единственно возможные цифры для D и E – либо 6 и 7 (или наоборот), либо 5 и 7 (или наоборот).

Предположим, что это 6 и 7. E – это или 6, или 7. Но мы пришли к противоречию, так как E + 1 = N, а значит, N тоже равно 7, а разные буквы, по условиям задачи, не могут обозначаться одной цифрой. С другой стороны, если E = 7, то уравнение E + 1 = N говорит нам о том, что N = 8, но 8 уже занято буквой R.

Таким образом, D и E – это либо 5 и 7, либо 7 и 5.

Но E не может быть равным 7 по той же причине, что и выше, иначе это означало бы, что N = 8, а это невозможно. Получается, D = 7, E = 5, Y = 2 и N = 6.

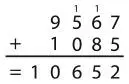
К тексту

Шаг 1. Буква T должна обозначать 1, поскольку сумма двух шестизначных чисел равна семизначному числу, которое начинается с 1. (Здесь мы можем не принимать во внимание роль четырехзначного числа, так как оно не может превратить общую сумму в семизначное число, начинающееся с цифры 2 или больше. Учитывая, что каждая буква представляет отдельную цифру, максимальное значение для DOUBLE + DOUBLE + TOIL – 987 543 + 987 543 + 6824 = 1 981 910.)

Шаг 2. Решение головоломок из разряда альфаметики требует повышенного внимания к переносу чисел. В каждом столбце может быть цифра 1, перенесенная из столбца справа. А при сложении в каждом столбце может получиться цифра 1, которую следует перенести в столбец слева.

Рассмотрим столбец, соответствующий разряду тысяч. Нам нужно сложить U + U + 1 (вместе с возможным переносом из суммы в столбце сотен), а ответ должен равняться числу, в котором есть буква U в столбце единиц.

Методом исключения можно сделать вывод, что буква U может обозначать только 8, если есть перенос, поскольку 8 + 8 + 1 + 1 = 18, или 9 – если переноса нет, так как 9 + 9 + 1 = 19. В обоих случаях 1 переносится в столбец 10 тысяч.

Шаг 3. Теперь проанализируем столбец 10 тысяч. Мы знаем, что сумма O + O + 1 равна числу, в столбце единиц которого есть О. Единственно возможное значение – О = 9, притом что 1 переносится в столбец сотен. А поскольку цифра 9 теперь занята, U = 8; согласно нашим вычислениям, перенос требуется и в столбце тысяч.

Шаг 4. В столбце сотен в ответе есть буква В в разряде единиц. И есть две возможные суммы – либо B + B + 9, либо (если в этом столбце есть перенос) B + B + 9 + 1. В первом случае В – это 1, а во втором В – 0. Поскольку буква T представляет 1, буква В должна иметь значение 0, и в этом столбце есть перенос 1.