Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Далее, строка 7 по горизонтали содержит либо слово THREE, либо слово EIGHT. К настоящему моменту мы использовали 12 букв: E, F, H, I, N, O, R, S, T, U, V и X. Поскольку нам известно, что в данном кроссворде присутствует только 12 букв, это позволяет исключить слово EIGHT, потому что в нем есть буква G. Следовательно, в строке 7 по горизонтали – THREE Vs.

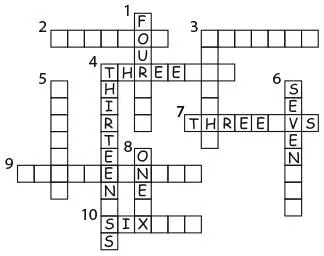
Шаг 4. В строке 3 по вертикали должно быть записано FOUR Hs, так как, если бы в ней было слово FIVE, в строке 4 по горизонтали было бы THREE Vs – то же самое, что и в строке 7 по горизонтали, а это противоречит тому, что в кроссворде 12 строк для 12 разных букв. Поскольку E самая распространенная из оставшихся букв, в строке 9 по горизонтали должно быть THIRTEEN Es. Это не может быть FOURTEEN, иначе в строке 5 по вертикали было бы несколько букв U, а буквы U уже учтены в строке 4 по горизонтали. И это не может быть EIGHTEEN, так как в кроссворде нет букв G, или NINETEEN, потому что в оставшихся клетках не поместится 19 букв E. Каждое из оставшихся трех чисел обозначается словом из четырех букв. Поскольку у нас уже есть строка THREE Vs, но в кроссворде только одна буква V, в двух из оставшихся строк должно быть слово FIVE. Так как в кроссворде есть строка THREE Us и только две буквы U, последняя строка должна содержать слово FOUR. Следовательно, всего в кроссворде четыре буквы О, а это значит, что в строке 2 по горизонтали должно быть FOUR Os, в строке 5 по вертикали – FIVE Is, в строке 3 по горизонтали – FIVE Fs, а в строке 10 по горизонтали – SIX Ts. В оставшихся клетках строк 1 по вертикали и 6 по вертикали расположились буквы N и R.

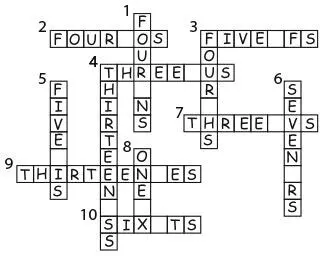
К тексту

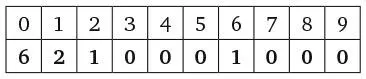
Я буду придерживаться системного подхода к решению этой задачи, начав с явно неверных путей и постепенно приближаясь к искомому ответу. Итак, нам нужно заполнить вторую строку таблицы так, чтобы каждая цифра обозначала частоту встречаемости верхней цифры в этой строке.

Начнем с цифры 9.

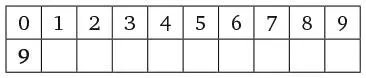
В таком случае в этом числе должно быть девять цифр 0, а значит, все остальные цифры тоже 0. Но мы знаем, что есть минимум одна цифра 9, так что все остальные цифры не могут быть 0.

Допустим, наше число начинается с цифры 8.

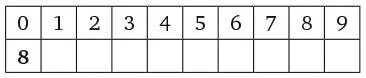
Это значит, что в оставшихся восьми клетках находится восемь цифр 0. Поскольку у нас есть минимум одна цифра 8, то цифра, которая размещена под ней (назовем ее х ), должна быть отличной от ноля, следовательно, во всех остальных ячейках находятся цифры 0.

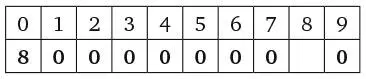
Подходящего значения х не существует! Это не 1, поскольку, по условиям задачи, на второй позиции должна быть цифра 0, указывающая на то, сколько раз цифра 1 встречается в итоговом числе. К такому же противоречию приводят и другие возможные значения х.

Прежде чем продолжить, выведем одно свойство цифр, расположенных во второй строке: в сумме они должны равняться десяти, так как каждая цифра во второй строке говорит о том, сколько раз в ней встречается определенная цифра. В строке десять позиций, следовательно, общая сумма цифр должна составлять десять.

Теперь допустим, что искомое число начинается с цифры 7.

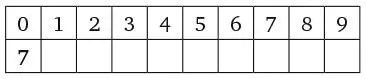
Мы знаем, что во второй строке семь нолей. А поскольку в искомом числе есть цифра 7, нам известно и то, что цифра под цифрой 7 в первой строке должна быть отличной от ноля и иметь значение 1, 2 или 3. (Если бы эта цифра была больше 3, сумма цифр была бы больше 10.) Однако в каждом из этих случаев решение неверное. Если под цифрой 7 находится цифра 1, то под цифрой 1 должна быть цифра, отличная от ноля. Это не может быть 1, так как тогда у нас было бы две цифры 1 в итоговом числе. Под цифрой 7 не может быть и 2, потому что тогда под цифрой 2 была бы цифра, отличная от ноля, а это противоречит тому, что в итоговом числе семь цифр 0. На основании аналогичных логических суждений делаем вывод, что под цифрой 7 не могут быть записаны цифры 2 и 3.

Проанализируем вариант с цифрой 6.

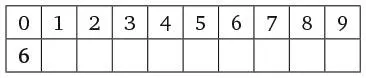
В итоговом числе шесть нолей. Под цифрой 6 находится цифра, отличная от ноля. Предположим, это 1.

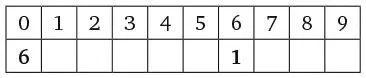
Таким образом, под цифрой 1 находится цифра, отличная от ноля. Поскольку сумма цифр в нижней строке должна равняться 10, под цифрой 1 может быть 1, 2 или 3. Мы можем исключить 1, так как это означало бы, что в нижней строке две цифры 1, что является противоречием. Если бы это была цифра 2, под ней должна быть цифра 1, чтобы сумма цифр составляла 10. Это выглядит многообещающе! У нас остается шесть пустых ячеек, в которых должно быть шесть цифр 0. Задача решена.

К тексту

Количество возможных комбинаций десяти цифр составляет 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3 628 800. Каждая из этих комбинаций представляет собой панцифровое число, за исключением тех, что начинаются с цифры 0, поскольку панцифровое число не может начинаться с ноля. (Комбинации десяти цифр, в которых первую позицию занимает цифра 0, считаются девятизначными числами.) Таких комбинаций 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 362 880. Следовательно, всего существует 3 628 800–362 880 = 3 265 920 панцифровых чисел.

К тексту

Мы будем перебирать цифры по одной и начнем с самого простого случая. Любое число, кратное 10, должно заканчиваться на 0, поэтому j = 0. Любое число, кратное 5, должно заканчиваться либо на 0, либо на 5. Следовательно, e = 5. При двух известных цифрах наше число – это abcd 5 fghi 0.

Если то или иное число делится на четное число, то оно и само должно быть четным. А значит, b, d, f и h тоже должны быть четными. Таким образом, b, d, f и h могут иметь значения 2, 4, 6 и 8. Следовательно, оставшиеся неизвестные a, c, g и i должны представлять собой ту или иную комбинацию из оставшихся (нечетных) цифр 1, 3, 7 и 9.

Теперь применим признак делимости на 4. Комбинации цифр, в которых c нечетное, d четное (что известно из предыдущего абзаца), а cd делится на 4, – это 12, 16, 32, 36, 72, 76, 92 и 96. Следовательно, d – это либо 2, либо 6.