Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления
- Название:Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2021
- Город:Москва
- ISBN:9785001468493
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления краткое содержание
Это книга для тех, кто интересуется математикой и логикой и любит разгадывать головоломки.
На русском языке публикуется впервые.
Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
В этой головоломке три элемента – два гвоздя и веревка, и если удалить один из них, то все три тут же отделяются друг от друга. Трудность лишь в том, чтобы понять, как представить два гвоздя и веревку в виде колец Борромео, поскольку ни гвозди, ни веревка совсем на них не похожи.
Давайте еще раз поразмышляем о кольцах Борромео. Например, это могут быть круговые кольца или треугольники валькнута. Вообще-то кольца Борромео могут иметь любую форму, какую мы захотим им придать, если только они сцеплены одинаковым способом. Представьте, что каждый гвоздь – это часть жесткого кольца, которое начинается с кончика гвоздя, проходит через стену, затем поднимается вверх и возвращается в комнату, после чего замыкается в конце гвоздя. Теперь вообразите, что оба конца веревки соединяются, образуя гигантскую петлю по всей комнате. Если эти три «кольца» сцеплены тем же способом, что и кольца Борромео, то удаление одного гвоздя приведет к тому, что веревка перестанет опоясывать петлей второй гвоздь, – и задача решена.
Как же это сделать? Я сам изготовил набор колец Борромео с помощью двух пластиковых колец и веревки, как показано на рисунке ниже. Затем я разделил кольца, поместив их бок о бок (как показано на рисунке справа), как будто это гвозди на стене. Способ образования веревкой петли между кольцами представляет собой решение задачи; оно изображено на нижнем рисунке.
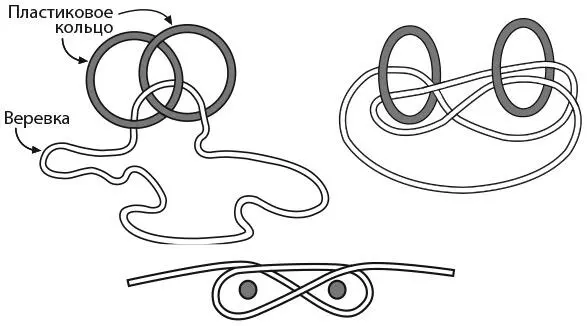
Обратите внимание: нас интересуют только те фрагменты каждого «кольца», которые изображены на этом рисунке, так как именно на нем показана связь между кольцами. Другие фрагменты «колец» – продолжение гвоздей, проходящее сквозь стену, или веревка, охватывающая всю комнату, – не имеют значения.
К тексту
44. ПРИМЕЧАТЕЛЬНОЕ КОЛЬЦО ДЛЯ САЛФЕТОКДавайте закончим начатое. Поскольку высота кольца для салфеток составляет 6 сантиметров, ее половина равна 3 сантиметрам. Следовательно, высота купола h равна r – 3, как показано на рисунке поперечного сечения ниже.
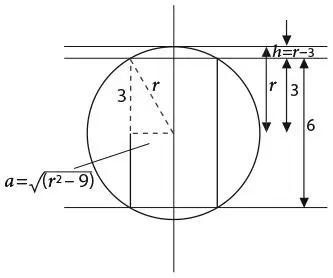
Для поиска a (радиус цилиндра, подлежащего удалению) мы применим теорему Пифагора к прямоугольному треугольнику, изображенному пунктирной линией. Квадрат гипотенузы равен сумме квадратов двух других сторон, то есть r 2 = a 2 + 3 2, а значит, 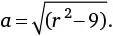
А теперь пора потрудиться. Мы уже нашли формулу объема кольца для салфеток: шар – цилиндр – 2 × купол.
Воспользовавшись ею, получим
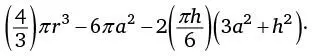
Подставим в это выражение вместо a и h их значения, выраженные через r :
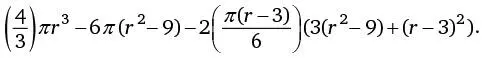
Раскрыв скобки, получим
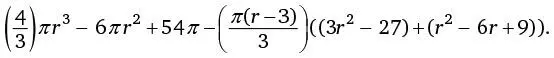
Продолжим:
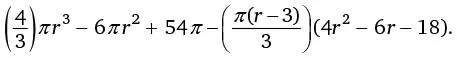
Осталось еще немного:
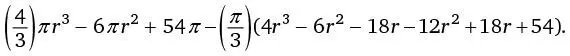
Простите за утомительную работу.
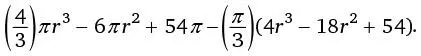
Почти готово!
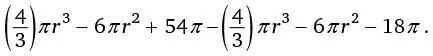
Сокращаем члены выражения, содержащие r , и получаем 36 π.
Ответ поражает воображение. Переменная r в нем отсутствует, а значит, в задаче размер шара вообще не имеет значения!
Все кольца для салфеток высотой 6 сантиметров имеют объем 36 π. Кольцо для салфеток высотой 6 сантиметров, полученное путем высверливания отверстия в шаре размером с апельсин, имеет такой же объем, как и кольцо, сделанное из шара размером с пляжный мяч или даже с Луну.
Увеличивая радиус кольца, вы делаете его тоньше, при этом такие факторы, как увеличение радиуса и уменьшение толщины кольца, полностью компенсируют друг друга для шаров всех размеров. Этот факт просто взрывает мозг!
К тексту
45. НЕРАЗБЕРИХА С ПЛОЩАДЯМИДополните рисунок с помощью пунктирных линий. Размер прямоугольника A и прямоугольника площадью 24 см 2составляет 9 × 5 = 45 см 2, поэтому A = 45–24 = 21 см 2. При этом A + B = 5 × 8 = 40 см 2. Следовательно, B = 19 см 2.
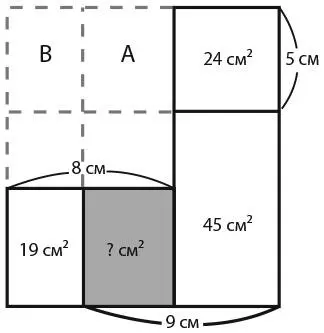
Прямоугольник B имеет аналогичную ширину и площадь, что и расположенный под ним прямоугольник площадью 19 см 2. Следовательно, его высота такая же и он должен быть идентичен этому прямоугольнику. Стало быть, у прямоугольника A та же высота и ширина, что и у прямоугольника, площадь которого мы вычисляем, а соответственно, и его площадь. Ответ: 21 см 2.
К тексту
46. ПРЯМОУГОЛЬНИКИ
К тексту
47. КИТАЙСКАЯ СТЕНА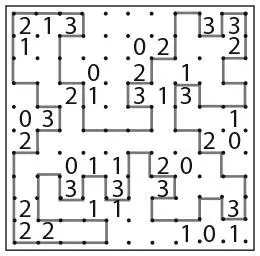
К тексту
48. АДСКИЙ ГОЛЬФ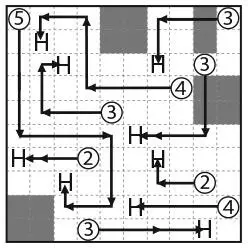
К тексту
49. СВЕТ
К тексту
50. ТЕМНАЯ КОМНАТАСуществует много решений этой головоломки, и все они построены по одному принципу. Комната с минимальным количеством стен – это комната с шестью стенами, напоминающая сюрикэн («лезвие, скрытое в руке» – япон.) с тремя зубцами – метательное оружие японских воинов в форме звезды. Квадратная комната более реалистична с архитектурной точки зрения.
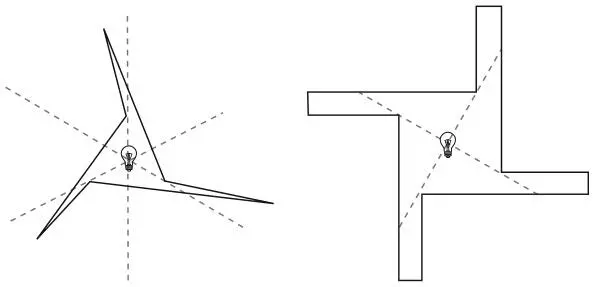
К тексту
1. E.
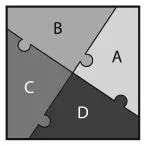
К тексту
2. г) 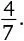 .
.
Эта задача решается несколькими способами. Например, можно привести все дроби к общему знаменателю 630. Так, 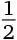 – это
– это 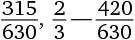 и т. д. Или записать их в десятичной форме. Поскольку значение этих дробей близко к
и т. д. Или записать их в десятичной форме. Поскольку значение этих дробей близко к 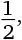 , можно проанализировать значение каждой дроби минус
, можно проанализировать значение каждой дроби минус 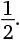 . В исходном порядке эти значения расположены следующим образом: 0,
. В исходном порядке эти значения расположены следующим образом: 0, 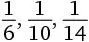 и
и 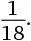 . Значит, в порядке возрастания дроби должны располагаться так:
. Значит, в порядке возрастания дроби должны располагаться так: 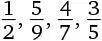 и
и 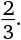 .
.
Интервал:
Закладка:









