Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

В анализе производная обозначается dy / dx . Предполагается, что это напомнит вам об обычной скорости изменений Δ y / Δ x , но теперь изменения dy и dx считаются бесконечно малыми. Это новая дикая идея, с которой мы будем работать медленно и осторожно, хотя она и не должна вызывать удивления. Мы знаем из принципа бесконечности, что путь к успеху в решении сложной задачи состоит в ее делении на бесконечно малые кусочки, их анализе и последующем сложении обратно с целью найти ответ. В контексте дифференциального исчисления небольшие изменения dy и dx – это те самые бесконечно малые кусочки. Их объединение – уже задача интегрального исчисления.

Чтобы подготовиться к тому, что нас ждет впереди, нужно с самого начала представлять общую картину. В анализе есть три центральные задачи. Они схематически показаны на диаграмме ниже.

1. Прямая задача: дана кривая, найти ее наклон в любой точке.

2. Обратная задача: дан наклон кривой в любой точке, найти кривую.

3. Задача площади: дана кривая, найти площадь лежащей под ней области.

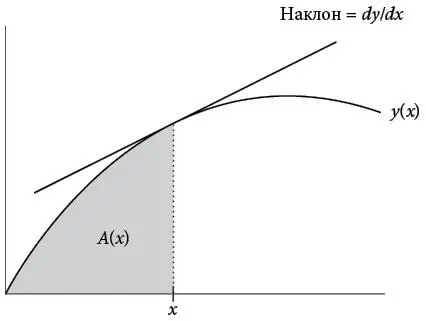
На диаграмме представлена некая обобщенная функция y ( x ). Я не уточнял, что означают y или x , потому что это не имеет значения. Картинка отражает обобщенность – она просто изображает некоторую кривую на плоскости. Эта кривая может представлять любую функцию одной переменной, и поэтому ее можно применять в любой области математики, где используются такие функции, то есть фактически везде. Значимость наклона и площади я объясню позже. Сейчас же думайте о них так, как есть: это наклон и площадь, то есть те вещи, которые интересуют геометров.

Мы можем рассматривать эту кривую двумя способами – старым и новым. В начале XVII века, до появления анализа, такие кривые считались геометрическими объектами, интересными сами по себе. Математики стремились количественно выразить их геометрические характеристики. Получив какую-то кривую, они хотели иметь возможность вычислять угол наклона касательной в каждой точке, длину дуги кривой, площадь под кривой и так далее. В XXI веке нас больше интересует функция, которая создала эту кривую, – функция, моделирующая какое-то природное явление или технологический процесс, в итоге отраженные в этой кривой. Кривая – это данные, но в их основе лежит нечто более глубокое. Сегодня мы думаем о кривой как о следах на песке, как о намеках на какой-то процесс, ее породивший. Мы интересуемся именно этим процессом (который моделируется функцией), а не следами, которые он после себя оставил.

Столкновение этих двух точек зрения – это столкновение загадки кривых и загадки движения и изменения. Именно так античная геометрия столкнулась с современной наукой. Хотя мы живем в нынешние времена, я предпочел рисовать картину исходя из старой точки зрения, потому что координатная плоскость прекрасно нам знакома. Она предлагает самый понятный способ восприятия трех центральных задач анализа, поскольку все они могут быть легко и наглядно представлены в геометрических терминах. (Те же идеи можно переформулировать в терминах движения и изменений с помощью динамических идей, например, используя скорость и расстояние вместо кривых и наклонов, однако мы сделаем это позже, когда лучше разберемся в геометрии.)

Эти вопросы следует интерпретировать в смысле функций. Иными словами, когда я говорю о наклоне кривой, я не имею в виду наклон в одной конкретной точке, а подразумеваю произвольную точку x . Наклон меняется, когда мы движемся вдоль кривой. Наша цель – понять, как он меняется в зависимости от точки x . Аналогично площадь под кривой также зависит от точки x . Я закрасил ее серым и обозначил x . Эту площадь также следует рассматривать как функцию от A ( x ). По мере увеличения x вертикальная пунктирная линия сдвигается вправо и площадь увеличивается. Поэтому она зависит от выбранного значения x .

Таковы три главные задачи. Как можно узнать меняющийся наклон кривой? Как мы можем восстановить кривую по известному наклону? И как вычислить переменную площадь под кривой?

В контексте геометрии эти задачи могут показаться довольно сухими. Но как только мы взглянем на них с точки зрения XXI века как на задачи реального мира, движения и изменения, они приобретают феноменальный масштаб. Наклоны измеряют скорость изменений, площади – накопление изменений. Наклоны и площади возникают в любой области – физике, инженерии, финансах, медицине, словом, везде, где к ним есть интерес. Понимание этих задач и их решений открывает вселенную современного количественного мышления, по крайней мере в отношении функций одной переменной. Для полной ясности я должен упомянуть, что анализ включает гораздо больше: функции многих переменных, дифференциальные уравнения и тому подобное. Но всему свое время. Мы вернемся к ним позже.

В этой главе рассматриваются функции одной переменной и их производные (скорости их изменений); мы начнем с функций, которые меняются с постоянной скоростью, а затем перейдем к более сложным функциям, меняющимся с переменной скоростью. Именно тут дифференциальное исчисление показывает себя во всей красе – оно придает смысл постоянным изменениям.

Освоившись со скоростью изменений, мы будем готовы заняться их накоплением, более сложной темой следующей главы. Там будет установлено, что прямая и обратная задачи, какими бы разными они ни казались, – это разлученные при рождении близнецы, и этот потрясающий результат называется основной теоремой анализа . Она показывает, что скорость изменений и их накопление связаны гораздо теснее, чем можно было подозревать, – открытие, которое объединило обе части анализа.

Однако начнем со скоростей изменений.

Многие повседневные ситуации можно описать линейной зависимостью – когда одна переменная пропорциональна другой. Например:

1. Прошлым летом моя старшая дочь Лия получила свою первую работу в магазине одежды. Она зарабатывала 10 долларов в час, поэтому за два часа ей платили 20 долларов. В общем случае, когда она работала t часов, она зарабатывала 10 t долларов.

2. Автомобиль едет по автостраде со скоростью 60 километров в час. Поэтому за один час он пройдет 60 километров, за два часа – 120 километров, а за t часов – 60 t километров. Взаимосвязь здесь такова: y = 60 t , где y – количество километров, пройденных за t часов.