Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Обратите внимание, что здесь мы используем принцип бесконечности – пытаемся упростить сложную кривую, нарезая ее на бесконечно маленькие отрезки. Именно это всегда происходит в анализе. Искривленные формы сложны; прямые формы просты, даже если их бесконечно много и они бесконечно малы. Вычисление производных таким способом – квинтэссенция математического анализа и одно из самых фундаментальных применений принципа бесконечности.

Чтобы провести этот мысленный эксперимент, нам нужно выбрать точку на параболе, в которой мы начнем проводить увеличение. Подойдет любая, но для численного удобства возьмем ту, которая соответствует значению x = 1 / 2. На рисунке выше она выделена. Ее координаты на плоскости таковы: (1/2, 1/4), или в десятичной записи (0,5; 0,25). Почему здесь y = 1 / 4? Мы выбираем точку, чтобы она лежала на параболе, а для всех точек ( x, y ) параболы должно выполняться соотношение y = x 2. Следовательно, в точке x = 1 / 2 значение y должно быть равно

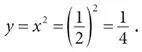
Теперь мы готовы производить увеличение в интересующей нас точке. Поместим точку ( x, y ) = (0,5;0,25) в центр поля микроскопа и с помощью компьютерной графики увеличим вокруг нее маленький участок кривой. На следующем рисунке показано первое увеличение.

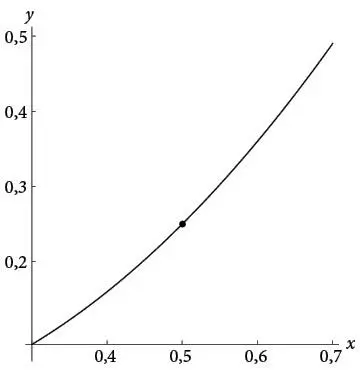
При таком увеличении общая форма параболы теряется. Мы видим слегка искривленную дугу. Этот небольшой кусок параболы, лежащий между x = 0,3 и x = 0,7, кажется намного менее искривленным, чем парабола в целом.

Продолжим увеличение, взяв участок от x = 0,49 до x = 0,51. Получившаяся в результате линия выглядит еще более прямой, чем предыдущий отрезок, – едва ли не по-настоящему прямой линией, хотя это все еще маленькая часть параболы.

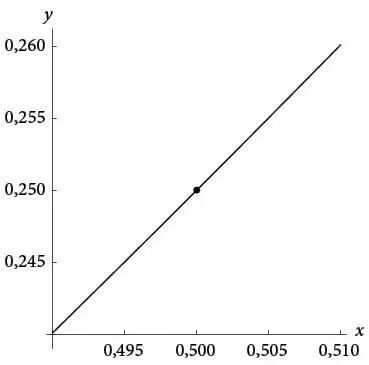
Тенденция ясна. По мере увеличения изображения участки параболы будут выглядеть все прямее. Измеряя отношение Δ y / Δ x для этого почти прямого участка и увеличивая все сильнее и сильнее, мы можем найти предельное значение наклона Δ y / Δ x , когда Δ x стремится к 0. Компьютерная графика настойчиво подсказывает, что наклон (угловой коэффициент) этой почти прямой линии становится все ближе к 1, что соответствует прямой под углом 45°.

С помощью алгебры мы можем доказать, что предельный наклон в точности равен 1. (В главе 8мы покажем, как производятся подобные вычисления.) Более того, выполнение такого расчета не только для точки x = 0,5, но и для любой точки x показывает, что предельный наклон – а значит, и угловой коэффициент касательной – равен 2 x для любой точки ( x, y ) параболы. На языке анализа это звучит так:

Производная функции x 2равна 2 x .

Как бы ни был велик соблазн доказать это правило для производных, прежде чем двигаться дальше, давайте пока примем его и посмотрим, что оно означает. Прежде всего, оно говорит, что в точке x = 0,5 наклон равен 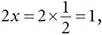что мы и видим на рисунке. Оно также утверждает, что в нижней точке параболы в x = 0 наклон должен равняться 2 × 0 = 0, и мы убедились, что это тоже верно. Наконец, формула 2 x говорит, что по мере движения по параболе вправо ее наклон будет возрастать; чем больше увеличивается x , тем больше должен быть наклон (= 2 x ), а это означает, что парабола должна становиться все круче и круче. Так на самом деле и есть.

Наш эксперимент помогает понять пару важных оговорок. Производная определена только в том случае, если по мере увеличения кривая приближается к какой-то предельной прямой линии. Это не относится к некоторым патологическим кривым. Например, если кривая имеет V-образную форму с острым углом в какой-то точке, то, как ни увеличивай окрестность этой точки, она продолжит выглядеть как угол. Этот угол никогда не исчезнет, независимо от степени увеличения кривой. Прямой линии никогда не получится. Следовательно, V-образная кривая не имеет определенной касательной в этом угле, и поэтому у нее нет тут производной.

Если же кривая выглядит все более прямой при достаточном увеличении, то говорят, что она гладкая В этой книге я исхожу из предположения, что кривые и процессы гладкие, как это делали родоначальники анализа. Однако в современном анализе мы научились справляться и с негладкими кривыми. Неудобства и патологии негладких кривых иногда возникают в областях, где бывают внезапные скачки или иные разрывности в поведении физических систем. Например, когда мы щелкаем выключателем электрической цепи, ток от состояния полного отсутствия внезапно переходит к состоянию наличия. График зависимости тока от времени показал бы резкий, почти вертикальный подъем, который аппроксимируется разрывным скачком в момент включения. Иногда удобнее смоделировать этот резкий переход как истинный разрыв значений функции, и в этом случае ток как функция времени не будет иметь производной в момент щелчка выключателем.

Значительная часть курса анализа в школе или колледже посвящена правилам вычисления производных, подобных установленным нами выше для x 2, только для других функций, таких как «производная синуса равна косинусу» или «производная ln x равна 1/ x ». Однако для наших целей более важно понять идею производной и увидеть, как это абстрактное определение применяется на практике. Для этого давайте обратимся к реальному миру.

В главе 4мы рассматривали данные о сезонных изменениях продолжительности дня. Тогда нам нужно было проиллюстрировать идею о синусоидах, оптимальном подборе кривых и сжатии данных; сейчас мы можем использовать те же данные для иллюстрации различных скоростей изменений и применить производные к другим задачам.

Исходные данные относились к количеству минут светового дня (времени между восходом и заходом солнца) в Нью-Йорке в 2018 году. В этом контексте производная – это скорость, с которой удлинялись или укорачивались дни. Например, 1 января время от рассвета до заката составляло 9 часов, 19 минут и 23 секунды. 2 января оно было немного больше: 9 часов, 20 минут и 5 секунд. Эти дополнительные 42 секунды дневного света (что эквивалентно 0,7 минуты) – мера того, насколько быстро удлинялся световой день за те конкретные сутки года. Продолжительность дня увеличивалась со скоростью примерно 0,7 минуты в сутки.