Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Загадка мгновенной скорости восходит к истории математики и философии – примерно к 450 году до нашей эры, когда Зенон предлагал свои устрашающие парадоксы. Вспомните, что в апории об Ахиллесе и черепахе философ утверждал, что быстрый бегун никогда не обгонит медленного, хотя Болт и опроверг это тем вечером в Пекине. А в апории «Стрела» Зенон утверждал, что стрела в полете не может двигаться. Математики до сих пор окончательно не определились, что именно пытался донести до нас Зенон своими парадоксами, но я предполагаю, что его, как и Аристотеля и других греческих философов, беспокоили тонкости, связанные с понятием мгновенной скорости. Их беспокойство может объяснить, почему греческие математики всегда мало говорили о движении и изменении. Подобно бесконечности, эти неприятные темы, казалось, были изгнаны из вежливых бесед.

Спустя две тысячи лет после Зенона основатели дифференциального исчисления разгадали загадку мгновенной скорости. Их интуитивно понятное решение сводилось к определению мгновенной скорости как предела, а точнее, как предел средней скорости, вычисленной за все более короткие и короткие интервалы времени. Это похоже на то, что мы делали, когда увеличивали участок параболы. Тогда мы аппроксимировали все меньшие и меньшие кусочки кривой с помощью прямой, а затем задавались вопросом, что происходит в пределе при бесконечном увеличении. Изучив предельное значение наклона прямой, мы смогли определить производную в конкретной точке плавно изогнутой параболы.

Сейчас по аналогии мы хотели бы аппроксимировать нечто, плавно изменяющееся во времени: перемещение Усэйна Болта по беговой дорожке. Идея заключается в замене графика пройденного расстояния в зависимости от времени ломаной, которая состоит из отрезков, показывающих постоянную среднюю скорость за короткие интервалы времени. Если средняя скорость на каждом интервале стремится к какому-то пределу, когда интервалы становятся все короче, то это предельное значение мы и будем подразумевать под мгновенной скоростью в данный момент. Как и наклон в точке, скорость в определенный момент будет производной.

Чтобы добиться успеха, нужно предположить, что пройденное спринтером расстояние менялось плавно. В противном случае предел, который нас интересует, не будет существовать (как, собственно, и производная). Хотя интервалы станут укорачиваться, результаты не приблизятся ни к чему осмысленному. Но действительно ли расстояние плавно меняется как функция времени? Мы точно не знаем. У нас есть только данные о времени, затраченном Болтом на прохождение 10-метровых отрезков. Чтобы оценить его мгновенную скорость, нам нужно выйти за пределы этих данных и сделать обоснованное предположение о том, где он находился в моменты времени между этими точками.

Системный способ сделать такое предположение известен как интерполяция. Идея состоит в том, чтобы провести плавную кривую между доступными данными. Другими словами, мы хотим соединить точки не отрезками [193], как делали раньше, а наиболее правдоподобной гладкой кривой, проходящей через точки или хотя бы очень близко к ним. На эту кривую мы налагаем определенные ограничения: она должна быть плавной, не слишком сильно колебаться и проходить максимально близко ко всем точкам, а кроме того, показывать, что в начальный момент скорость Болта равнялась нулю, поскольку мы знаем, что на старте он был неподвижен. Этим критериям соответствуют много разных кривых. Статистики разработали массу методов для подбора кривых, отвечающих имеющимся данным. Все они дают сходные результаты, а учитывая, что они в любом случае предполагают какие-то допущения, не будем особо беспокоиться о том, какую кривую использовать.

Вот один пример плавной кривой, удовлетворяющей всем требованиям:

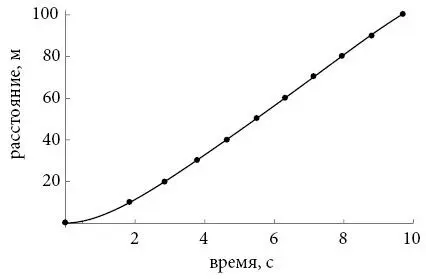
Поскольку эта кривая по определению гладкая, мы можем вычислить ее производную в каждой точке. Полученный график дает оценку скорости Усэйна Болта в каждый момент его рекордного забега в тот вечер в Пекине.

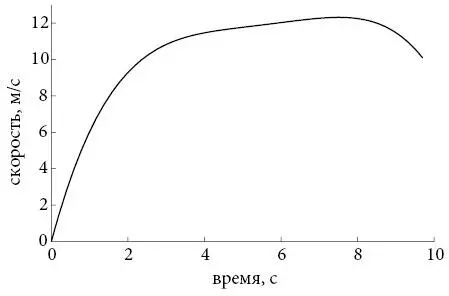
Исходя из графика, Болт достиг максимальной скорости около 12,3 метра в секунду примерно на трех четвертях дистанции. До этого бегун ускорялся, постоянно набирая скорость. Затем он замедлился настолько, что в момент пересечения финишной черты его скорость упала до 10,1 метра в секунду. График подтверждает то, что видели все: Болт резко сбавил темп в конце, особенно на последних двадцати метрах, когда расслабился и праздновал победу.

В следующем, 2009-м, году на чемпионате мира в Берлине Болт положил конец спекуляциям о том, насколько быстро он может бегать. На этот раз никаких жестов и ударов в грудь. Он со всем усердием добежал до финиша и побил свой пекинский рекорд 9,69, показав еще более удивительный результат – 9,58 секунды. Поскольку событие было ожидаемым, специалисты по биомеханике приготовили лазерное оборудование [194], сходное по действию с радарами, используемыми полицией для ловли водителей-лихачей. Эти высокотехнологичные инструменты позволяли измерять положение спринтеров сто раз в секунду. Когда они вычислили мгновенную скорость Болта, получились такие результаты:

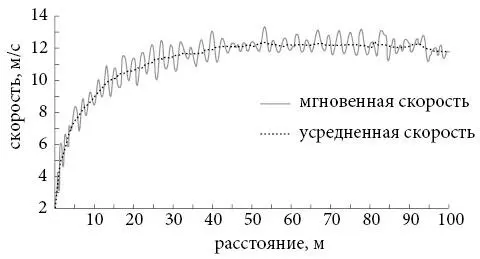
Незначительные колебания вокруг общего тренда отражают увеличения и снижения скорости, которые неизбежны во время бега. В конце концов, бег – это серия отталкиваний и приземлений. Скорость Болта немного менялась каждый раз, когда он приземлялся ногой на землю, притормаживал, а затем снова толкал себя вперед и взмывал в воздух. Какими бы интригующими ни были такие колебания, они раздражают специалистов по аналитике данных. Мы желаем видеть тренд, а не мелкие вихляния, и для этой цели предыдущий подход с аппроксимирующей кривой был не хуже, а, возможно, и лучше. После сбора всех данных высокого разрешения и наблюдения колебаний специалистам все равно пришлось их чистить. Они фильтровали их, чтобы выявить более значимый тренд.

Мне такие колебания преподносят важный урок. Я рассматриваю их как метафору, своего рода поучительную басню о природе моделирования реальных явлений с помощью анализа. Если мы попытаемся зайти с разрешением в своих измерениях слишком далеко и начнем смотреть на любое явление в мучительно мелких деталях во времени или пространстве, то станем замечать нарушение гладкости. В данных о скорости Усэйна Болта колебания сделали общий тренд похожим на ершик для чистки труб. То же самое произошло бы с любой формой движения, если бы мы могли измерять его в молекулярном масштабе. На этом уровне движение становится дерганым и весьма далеким от плавности. Анализ больше не может нам много рассказать об этом, по крайней мере, непосредственно. Тем не менее, если нас волнуют общие тенденции, сглаживания колебаний может оказаться вполне достаточно. Понимание природы движения и изменений во Вселенной, которые дает анализ, – это доказательство мощи сглаженности, хотя она может быть всего лишь приблизительной.