Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Мы хотим знать, как далеко уедет машина за время t , если начать с момента 0. Иными словами, какой функцией времени определяется пройденное расстояние? Было бы ужасной ошибкой использовать школьную формулу, когда расстояние равно произведению скорости на время, поскольку она верна только для движения с постоянной скоростью, а в нашем случае это не так. Наоборот, у нас скорость увеличивается с каждой секундой. Мы больше не в сонном мире постоянных скоростей, а в захватывающем мире постоянного ускорения.

Ученые Средневековья уже знали ответ на этот вопрос. Уильям Хейтсбери, философ и логик из Мертон-колледжа в Оксфорде, решил эту задачу около 1335 года, а Николай Орем, французский теолог и математик, около 1350 года дополнительно разъяснил ее, представив наглядно. К сожалению, их работы не получили широкой известности и вскоре были забыты. Примерно 250 лет спустя Галилей показал, что равноускоренное движение – не какая-то абстракция. Именно так двигаются тяжелые предметы (например, металлические шары), когда падают на Землю или катятся по слегка наклонной плоскости. В обоих случаях скорость шаров растет пропорционально времени v = at , как и ожидается при движении с постоянным ускорением.

Итак, мы знаем, что скорость увеличивается линейно v = at . А как увеличивается расстояние ? Согласно основной теореме, пройденное расстояние равно площади под кривой скорости, накопленной к моменту t . Поскольку у нас кривая скорости – это наклонная прямая v = at , то соответствующую площадь нетрудно вычислить. Это площадь треугольника, изображенного ниже.

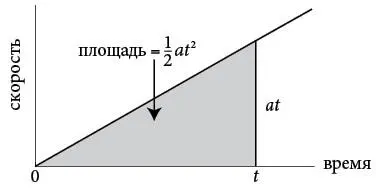
Как и серый прямоугольник в предыдущей задаче, серый треугольник тоже будет расширяться со временем вправо. Разница в том, что прямоугольник увеличивался строго горизонтально, а треугольник растет в обоих направлениях. Для вычисления площади заметим, что в любой момент времени основание треугольника равно t , а высота – текущей скорости объекта, то есть v = at . Поскольку площадь треугольника составляет половину произведения длины основания на высоту, она равна ½ × t × at = at 2 / 2. Согласно основной теореме площадь под кривой скорости говорит нам, какое расстояние прошло тело:

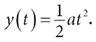
Итак, если тело начинает движение из состояния покоя, а затем равномерно ускоряется, то пройденное расстояние пропорционально квадрату затраченного времени. Именно это Галилей открыл экспериментально и очаровательным образом выразил в виде закона нечетных чисел, как мы видели в главе 3. Ученые в Средние века тоже это знали [202], [203].

Но вот чего не знали ни в Средневековье, ни даже во времена Галилея, так это того, как поведет себя скорость, если ускорение не будет простой константой. Другими словами, если нам известно, что тело двигается с произвольным ускорением a ( t ), то что можно сказать о его скорости v ( t )?

Это похоже на обратную задачу, о которой я упоминал в предыдущей главе. Чтобы правильно ее понять, крайне важно оценить, что мы знаем и чего не знаем.

Ускорение определяется как быстрота изменения скорости. Поэтому, если нам дана скорость v ( t ), то найти соответствующее ускорение a ( t ) просто. Это решение прямой задачи. Мы могли бы ее решить, вычислив быстроту изменения данной нам скорости во многом так же, как в предыдущей главе вычисляли наклон параболы, расположив ее под микроскопом. Чтобы найти скорость изменения известной функции, нужно всего лишь прибегнуть к определению производной и к правилам вычисления производных для различных функций.

Однако обратную задачу делает сложной именно то, что нам не дана функция скорости. Наоборот, нас просят ее найти. Предполагается, что у нас есть ускорение, то есть быстрота изменения скорости, в виде функции от времени, и нам нужно выяснить, какая именно функция скорости будет иметь такую быстроту изменений. Как нам решать задачу в обратном направлении , чтобы получить неизвестную скорость из известной быстроты ее изменений? Словно детская игра: «Я загадал функцию скорости, быстрота изменения которой такая-то и такая-то. Какую функцию скорости я загадал?»

Та же головоломка, связанная с необходимостью в обратных рассуждениях, возникает при попытке вывести расстояние из скорости. Так же как ускорение – это быстрота изменения скорости, скорость – это быстрота изменения расстояния. Рассуждать в прямом направлении просто: если мы знаем расстояние, пройденное двигающимся телом, как функцию времени, как в случае с Усэйном Болтом, бегущим по дорожке в Пекине, то нетрудно вычислить скорость тела в каждый момент времени. Мы выполнили такой расчет в предыдущей главе. Однако рассуждать в обратном направлении трудно. Если бы я сообщил вам скорость Усэйна Болта в каждый момент забега, вы бы смогли найти положение бегуна в каждый момент времени? В более общем виде: при наличии произвольной функции скорости v ( t ) вы бы смогли найти соответствующую функцию расстояния y ( t )?

Основная теорема Ньютона пролила свет на эту весьма трудную обратную задачу поиска неизвестной функции по данной скорости ее изменения и во многих случаях позволила полностью ее решить. Ключевой момент – переформулировать ее как вопрос о площадях, которые изменяются.

Доказательство основной теоремы с помощью малярного валика

Основная теорема анализа стала кульминацией восемнадцати веков развития математической мысли. С помощью динамических средств она ответила на статический геометрический вопрос, который Архимед мог задавать в Древней Греции в 250 году до нашей эры, или Лю Хуэй в Китае в 250 году, или ибн аль-Хайсам в Каире в 1000-м, или Кеплер в Праге в 1600-м.

Рассмотрим фигуру, подобную серой области на приведенном рисунке.

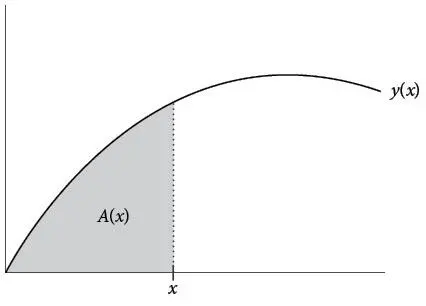
Есть ли способ точно вычислить площадь такой произвольной формы, как показанная на рисунке, учитывая, что кривая, ограничивающая ее сверху, может быть почти произвольной? В частности, это не обязательно должна быть классическая кривая. Это может быть некая экзотическая кривая, определяемая каким-нибудь уравнением на координатной плоскости – в джунглях, открытых Ферма и Декартом. А что, если эта кривая определена каким-то физическим процессом, например траекторией двигающейся частицы или луча света? Существует ли какой-то способ находить площадь под такой кривой и делать это системным образом? Такова задача площади – третья центральная задача анализа, о которой я упоминал ранее, и самая насущная математическая задача середины 1600-х годов. Это была последняя неразгаданная загадка кривых. Исаак Ньютон подошел к ней с новой стороны, используя идеи, подсказанные загадками движения и изменения.