Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Простейшая иллюстрация его идеи возвращает нас к знакомой задаче с автомобилем, движущимся с постоянной скоростью, для которого пройденное расстояние равно скорости, умноженной на время. Каким бы элементарным ни был этот пример, он все же отражает суть основной теоремы и поэтому подойдет для начала ее рассмотрения.

Представьте, что машина едет по шоссе со скоростью 60 километров в час. Если мы построим график зависимости расстояния от времени и график зависимости скорости от времени, то они будут выглядеть так:

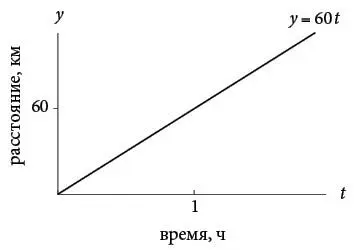
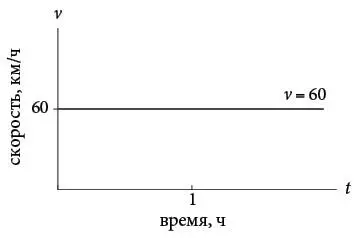
Сначала посмотрим на расстояние в зависимости от времени. Через один час автомобиль проедет 60 километров, через два часа – 120 километров и так далее. В целом расстояние и время связаны соотношением y ( t ) = 60 t , где y ( t ) – расстояние, пройденное за время t . Я буду называть y ( t ) = 60 t функцией расстояния. Как показано на верхнем рисунке, график функции расстояния – это прямая с наклоном (угловой коэффициент) 60 километров в час. Эта величина сообщает нам скорость автомобиля в любой момент (если бы мы ее еще не знали). В более сложных ситуациях скорость может меняться, но сейчас это простая постоянная функция, v ( t ) = 60 для любых значений t . Она отображена на нижнем рисунке в виде горизонтальной линии.

Посмотрев, как скорость проявляет себя на графике расстояния (как наклон прямой), теперь переиначим вопрос и спросим: как расстояние проявляет себя на графике скорости? Иными словами, есть ли на графике скорости какая-нибудь визуальная или геометрическая особенность, которая позволила бы нам увидеть, какое расстояние преодолел автомобиль за любое конкретное время t ? Да, есть. Пройденное расстояние – это площадь под кривой скорости (в нашем случае это прямая линия) до момента времени t .

Чтобы понять, почему это так, предположим, что машина проехала какое-то определенное время, например полчаса. В этом случае она проедет 30 километров, поскольку 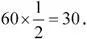Но суть всего этого в том, что мы можем узнать это расстояние в виде площади серого прямоугольника под прямой между моментами времени t = 0 и 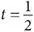часа.

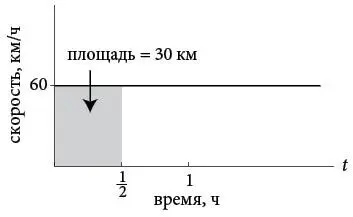
Высота этого прямоугольника – 60 километров в час, основание – 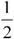часа. Это дает нам площадь 30 километров, что и будет пройденным расстоянием.

То же самое рассуждение работает для любого времени t . Основанием прямоугольника будет t , высота – по-прежнему 60, поэтому площадь равна 60 t . И действительно, именно это расстояние мы и ожидаем найти, y = 60 t .

Таким образом, как минимум в этом примере, где скорость всегда постоянна, а кривая скорости – просто прямая линия, ключ к определению пройденного расстояния – поиск площади под кривой скорости. Открытие Ньютона состояло в том, что это равенство между площадью и расстоянием верно всегда , даже если скорость непостоянна. Как бы неравномерно ни двигался объект, площадь под кривой скорости к моменту t всегда равна общему расстоянию, пройденному за время t. Это один из вариантов основной теоремы. Он кажется слишком простым, чтобы претендовать на истину, но тем не менее это она и есть.

Ньютон пришел к нему, думая о площади как о переменной величине, а не о фиксированной мере, как тогда было принято в геометрии. Он ввел в геометрию время, рассматривая ее как физику. Если бы Ньютон жил сегодня, возможно, он бы визуализировал приведенный выше рисунок с помощью анимации, например в виде кинеографа [201], а не мгновенного снимка. Чтобы сделать это, снова взгляните на картинку выше, но теперь представьте, что это один кадр фильма или одна страничка в кинеографе. Как будет меняться серый прямоугольник, если мы начнем просматривать анимацию? Мы увидим, что он расширяется вправо. Почему? Потому что длина его основания равна t и она увеличивается со временем. Если бы мы могли делать по кадру для каждого момента и последовательно их воспроизводить, словно пролистывая странички в кинеографе, то увидели бы, как анимированная версия серого прямоугольника расширяется вправо. Это походило бы на поршень или лежащий на боку шприц, который втягивает серую жидкость.

Эта серая жидкость представляет собой увеличивающуюся площадь прямоугольника. Мы представляем, что эта площадь «накапливается» под кривой скорости v ( t ). В нашем случае площадь, накопленная к моменту времени t , равна A ( t ) = 60 t , что совпадает с расстоянием, пройденным автомобилем, y ( t ) = 60 t . Таким образом, накопленная площадь под кривой скорости дает расстояние как функцию времени. Это вариант основной теоремы для движения.

Мы прокладываем дорогу к Ньютонову общему геометрическому случаю основной теоремы, в котором фигурирует произвольная кривая y ( t ) и площадь A ( t ) под ней. Идея накопления площади – ключевая для объяснения теоремы, но я понимаю, что к ней следует немного привыкнуть. Поэтому давайте применим ее еще к одной конкретной задаче о движении, прежде чем перейдем к общему случаю.

Рассмотрим объект, движущийся с постоянным ускорением. Это означает, что он перемещается все быстрее и быстрее с равномерно увеличивающейся скоростью. Это немного напоминает то, как вы нажимаете на педаль газа в своем автомобиле, и он разгоняется из состояния покоя. Через одну секунду машина достигнет скорости, предположим, 10 километров в час, через две – 20 километров в час, через три – 30 километров в час и так далее. В этом гипотетическом примере автомобиль каждую секунду добавляет к своей скорости 10 километров в час. Такое изменение скорости, 10 километров в час за секунду, называется ускорением автомобиля. (Для простоты проигнорируем тот факт, что машина не может ускоряться бесконечно и что ускорение не строго постоянно, когда вы давите на педаль газа.)

В нашем идеализированном примере скорость в любой момент времени задается уравнением v ( t ) = 10 t . Здесь число 10 означает ускорение автомобиля. Если бы ускорение было другой константой, допустим a , то формула приняла бы более общий вид v ( t ) = at .